Triangulació de Delaunay

Una triangulació de Delaunay /dəlo'ne/, de vegades escrit fonèticament «Deloné», és una xarxa de triangles que compleix la condició de Delaunay. Aquesta condició diu que la circumferència circumscrita de cada triangle de la xarxa no ha de contenir cap vèrtex d'un altre triangle. S'usen triangulacions de Delaunay en geometria per ordinador, especialment en gràfics 3D per computadora.

Es denomina així pel matemàtic rus Borís Nikolàeivitx Delaunay (Борис Николаевич Делоне, 1890 - 1980) de vegades transcrit "Deloné", qui el va inventar el 1934;[1] el mateix Delone va usar la forma francesa del seu cognom, «Delaunay», com mostra d'apreci als seus avantpassats francesos.

Aplicació

En gràfics 3D per computadora s'usen xarxes de polígons per modelar objectes tridimensionals, ajuntant els polígons per imitar la superfície de l'objecte. En general s'usen triangles perquè són els polígons més simples i tenen moltes propietats favorables, com que representen una superfície coplanar.

Hi ha dues maneres de modelar un objecte de superfícies: modelar a mà o escanejar amb un range escàner. Quan s'escaneja es produeix un relleu de la superfície format per punts discrets (vegeu Fig 1). Per utilitzar aquest relleu cal transformar-lo en una xarxa de triangles (vegeu Fig 2); aquesta transformació es diu «triangulació 3D» que cal distingir la triangulació emprada pels topògrafs.

La triangulació de Delaunay maximitza els angles interiors dels triangles de la triangulació. Això és molt pràctic perquè en usar la triangulació com a model tridimensional els errors d'arrodoniment són mínims. Per això, en general s'utilitzen triangulacions de Delaunay en aplicacions gràfiques.

  • Fig 1. D'alguns punts es vol construir una triangulació.
    Fig 1. D'alguns punts es vol construir una triangulació.
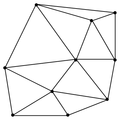  • Fig 2. És fàcil construir qualsevol triangulació simplement connectant els vèrtexs.
    Fig 2. És fàcil construir qualsevol triangulació simplement connectant els vèrtexs.
  • Fig 3. Amb la condició de Delaunay es pot examinar si la triangulació és útil.
    Fig 3. Amb la condició de Delaunay es pot examinar si la triangulació és útil.
  • Fig 4. Els tres vèrtexs A, B, C del triangle ABC estan a la mateixa distància del circumcentre O.
    Fig 4. Els tres vèrtexs A, B, C del triangle ABC estan a la mateixa distància del circumcentre O.
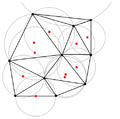  • Fig 5. La triangulació amb totes les circumferències circumscrites i els seus centres (en vermell).
    Fig 5. La triangulació amb totes les circumferències circumscrites i els seus centres (en vermell).
  • Fig 6. Connectant els centres de les circumferències circumscrites es produeix el diagrama de Voronoi (en vermell).
    Fig 6. Connectant els centres de les circumferències circumscrites es produeix el diagrama de Voronoi (en vermell).
  • Fig 7. Aquesta triangulació no compleix la condició de Delaunay.
    Fig 7. Aquesta triangulació no compleix la condició de Delaunay.
  • Fig 8. Aquesta triangulació no compleix la condició de Delaunay.
    Fig 8. Aquesta triangulació no compleix la condició de Delaunay.
  • Fig 9. Flipping de l'aresta comú produeix una triangulació que compleix la condició de Delaunay.
    Fig 9. Flipping de l'aresta comú produeix una triangulació que compleix la condició de Delaunay.

Vegeu també

Referències

A Wikimedia Commons hi ha contingut multimèdia relatiu a: Triangulació de Delaunay
  1. ↑ B. Delaunay: Sud la sphere vide. A la mémoire de Georges Voronoi. Izvestia Akademii Nauk SSSR, Otdelenie Matematicheskikh i Estestvennykh Nauk (Bulletin of Academy of Sciences of the USSR), 7, pàg. 793-800, 1934