Formule de Steiner-Minkowski

Pour les articles homonymes, voir Steiner et Minkowski.
En géométrie, les formules de Steiner-Minkowski sont des relations traitant d'un compact C d'un espace euclidien E. On ajoute en général une condition supplémentaire sur le compact, indiquant qu'il est soit convexe, soit de frontière homéomorphe à la sphère et paramétrable par une fonction de classe C2 de la sphère dans l'espace euclidien.
La première formule indique que la frontière du compact est mesurable et que sa mesure est égale à la dérivée en 0 de la fonction de R+ dans lui-même, qui à un scalaire ε associe le volume de C + εB. Ici, R+ désigne l'ensemble des nombres réels positif, B la boule unité et le signe + la somme de Minkowski. La mesure utilisée est celle de Lebesgue.
La deuxième formule indique que la mesure du volume de C + εB s'exprime comme un polynôme de degré la dimension de E, si ε est suffisamment petit.
La mesure de la frontière utilisée correspond au contenu n – 1 dimensionnel de Minkowski. Dans le cas où la frontière est paramétrable par une fonction de classe C2, le contenu se confond avec la définition usuelle, c'est-à-dire celle obtenue avec la forme volume canonique. Dans le cas de la dimension 2, ce contenu, dans le cas où la frontière est convexe, se confond avec la longueur de l'arc qu'est la frontière, au sens de Jordan.
Les formules de Steiner-Minkowski sont utilisées conjointement avec le théorème de Brunn-Minkowski, pour prouver le théorème isopérimétrique. Elles ont été ainsi nommées en l'honneur des mathématiciens lituanien Hermann Minkowski et suisse Jakob Steiner.
Contenu de Minkowski
Une des difficultés de la première formule de Steiner-Minkowski, sous sa forme générale, est le sens à donner au mot mesure de la frontière. Comme le montre l'article longueur d'un arc, il existe différentes manières de définir cette mesure.
En dimension 2, si la frontière est le support d'un arc paramétré (I, f) injectif presque partout et de classe C1, une première définition de la mesure mf de cette frontière est la suivante :
Cette définition se généralise bien, en dimension finie quelconque, si la frontière est l'ensemble d'arrivée d'un homéomorphisme φ de classe C1 de la sphère Sn – 1. La mesure de la frontière s'exprime comme l'intégrale sur la sphère de la valeur absolue déterminant jacobien de la fonction φ :
Dans le cas d'un convexe compact d'un espace dimension 2, la frontière est toujours le support d'un arc paramétrée injectif presque partout. En revanche, cet arc n'est pas nécessairement de classe C1. Ceci n'est guère gênant, la définition de Jordan donne un sens à la longueur de l'arc, correspondant à une mesure 1 dimensionnel dans un espace de dimension 2. Dans le cas d'une dimension quelconque, la définition de Jordan ne se généralise pas (cf l'article Longueur d'un arc). Une autre définition prend le relai, celle du contenu n-1 dimensionnel de Minkowski.
- Le contenu p-dimensionnel de Minkowski d'un ensemble K d'un espace euclidien de dimension n, si p est un entier plus petit que n est la limite Cp,K, si elle existe, définie par[1] :
Ici, μ désigne la mesure de Lebesgue, B la boule unité et Bn – p la boule unité d'un espace de dimension n – p.
Cette définition est bien cohérente avec les deux précédentes :
- Soit C un convexe compact de E, un espace vectoriel de dimension n. Si la frontière F de C est l'ensemble d'arrivée d'un homéomorphisme φ de classe C1 de la sphère Sn – '1, le contenu n – 1-dimensionnel de Minkowski Cn – 1,F de F vérifie l'égalité :
- Soit C un convexe compact de E, un espace vectoriel de dimension 2. Si la frontière F de C est le support de l'ensemble d'arrivée d'un lacet simple, le contenu 1-dimensionnel de Minkowski de C1,F de F est égal à la longueur du lacet simple au sens de Jordan.
Un lacet ([a, b], f) est un arc paramétré sur un segment [a, b] tel que l'image de a soit égal à l'image de b par f. Le lacet est dit simple si la restriction de f à [a, b] est injective.
Dimension 2
Dans ce paragraphe, K désigne un compact non vide de E, un espace euclidien de dimension 2 et μ la mesure de Lebesgue de E. En dimension 2, les preuves sont plus aisées. La première formule de Steiner-Minkowski s'énonce ainsi :
- Si K est convexe ou si sa frontière est le support d'un lacet simple de Jordan, la mesure de K + εB s'exprime comme un polynôme de degré 2 en ε. Ici ε désigne un nombre réel positif suffisamment petit :
Dans le cas où K désigne un convexe, la valeur positive ε peut être choisie quelconque. La deuxième formule de Minkowski donne une expression du périmètre de K :
- Si K est convexe ou si sa frontière est le support d'un lacet simple de Jordan, la frontière de K est le support d'un arc rectifiable au sens de Jordan et si désigne la longueur de la frontière de K :
La deuxième formule de Minkowski indique que le coefficient p de la première formule est égal au périmètre de K. Dans le cas d'un convexe, le coefficient q est égal à π. Si la frontière est un lacet simple, on trouve une démonstration au paragraphe Formalisme de l'article Longueur d'un arc.
C désigne un compact convexe dans cette démonstration. Dans un premier temps, on établit l'égalité de Steiner-Minkowski uniquement pour les polygones convexes.
- Si P est un polygone d'aire égale à aP et de périmètre pP et si ε est un nombre réel positif :
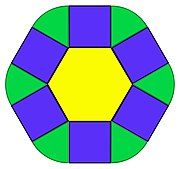
- Dans le cas d'un polygone convexe, la deuxième formule de Steiner-Minkowski est presque évidente, elle est illustrée par la figure en haut à droite, pour le cas d'un hexagone. On peut décomposer l'aire en trois parties. La partie jaune correspond à l'aire aP du polygone. La partie bleue est l'accroissement de surface au-dessus d'une arête, pour chaque arête on obtient une surface rectangulaire d'aire la longueur de l'arête que multiplie ε. Comme la somme des longueurs des arêtes est égale à pP, on trouve le terme εpP. Enfin, à chaque sommet, on trouve une portion de disque de rayon ε, représentant un angle θs. Comme parcourir le polygone revient à faire un tour complet, la somme des angles θs est égal à 2π, ce qui montre que la somme des aires des portions de disque correspond à l'aire d'un disque complet, de rayon ε.
Dans le cas général, le terme p, intervenant dans la formule à démontrer, désigne le périmètre du compact convexe C, il est nécessaire de montrer qu'il est fini.

- La frontière de C est rectifiable :
- Si l'intérieur de C est vide, trois points quelconques de C sont alignés sinon la convexité montre que le triangle de sommets ces trois points est inclus dans C et est d'intérieur non vide. C est inclus dans une droite. Comme il est convexe et compact, sa géométrie est celle d'un segment et la proposition est évidente.
- Si l'intérieur de C est non vide, on considère un point O de cet intérieur. Cette configuration est illustrée sur la figure de droite. Comme C est compact, il existe un réel positif a tel que le disque de centre O et de rayon a contienne C. On considère un cercle Cb de centre 0 et de rayon b strictement plus grand que a. Ce cercle est illustré en rouge sur la figure. L'objectif est de montrer qu'un polygone P convexe dont les sommets sont des points de la frontière de C est de périmètre plus petit que 2π.b. Le polygone P est illustré en bleu. Pour cela, on considère l'ensemble des segments d'extrémités le centre 0 et un point du cercle Cb frontière du disque, passant par un sommet de P. Ils sont illustrés en vert sur la figure. Soit E l'ensemble des polygones convexes dont les sommets sont tous sur les segments précédemment décrits. Si s est le nombre de sommets de P, on peut identifier E à une partie de [0, b]s, sous ensemble de Rs. Cette identification permet de munir E de la topologie induite par celle de Rs. L'ensemble E est alors un compact et la fonction qui associe son périmètre à un convexe est continue, elle admet au moins un maximum.
- On va montrer qu'il n'existe qu'un unique maximum M, correspondant au polygone illustré en rouge sur la figure et correspondant au point de coordonnées (b,..., b). Pour cela on montre qu'un polygone Pc ayant au moins une coordonnée strictement inférieure à b ne peut être de périmètre maximal dans E. Soit S2 ce sommet à une distance strictement inférieure à b de O et soit S1 et S3 les deux sommets précédents et suivant. Soit L2 le segment vert, contenant S2 et d'extrémité O et un point du cercle Cb. Comme les points de E correspondent à des convexes, le sommet S2 est dans la portion L2c de L2 d'extrémités, l'intersection de L2 avec [S1, S3], et un point du cercle. Tout polygone ayant même sommets que Pc à l'exception de S2, remplacé par un point de L2c est élément de E. Parmi ces polygones, celui de plus grand périmètre est celui pour lequel S2 est remplacé par un point du cercle Cb. Le polygone Pc possède un périmètre strictement majoré, il n'est donc pas maximal. Le seul polygone de périmètre maximal possible est M, comme par ailleurs, nous savons qu'il existe un polygone de périmètre maximal dans E, il correspond nécessairement à M.
- Le polygone P est de périmètre majoré par celui de M, lui-même majoré par 2π.b. On en déduit que toute ligne polygonale approximant le convexe C est majoré par 2π.b, ce qui montre que la frontière est bien rectifiable.
On appelle p le périmètre de C, qui est une grandeur finie d'après la démonstration précédente. On montre ensuite qu'il est possible d'approcher C par un polygone compact convexe. La lettre η désigne un réel strictement positif.
- Il existe un polygone compact convexe P inclus dans C, à une distance de Hausdorff inférieure à η de C et tel que les périmètres et les aires de C et de P diffèrent de moins de η :
- On choisit un polygone convexe dont les sommets sont des points de C et qui approxime le périmètre de C à η près. Quitte à ajouter des points, on choisit le polygone tel qu'aucune arête ne soit de longueur l, supérieure à 1 ou à η/(p + π). Ce polygone est noté P. La surface P + l.B contient le convexe C, la démonstration est proposée dans l'article Théorème isopérimétrique au paragraphe Polygone et Steiner. Ceci montre que la distance de Hausdorff entre P et C est inférieure à η. L'aire μ(P + l.B) est plus grande que celle de C car C est contenu dans P + l.B. La formule de mesure d'une telle aire pour un polygone et le fait que le périmètre de P soit plus petit que celui de C montre que :
La formule est maintenant établit pour les polygones et il existe un polygone proche de C, à la fois en surface et en périmètre. Dans la démonstration suivante, ce polygone permet de montrer que la première formule de Steiner Minkowski est vraie aussi pour C. Si la frontière est un lacet simple, on trouve une démonstration dans l'article Longueur d'un arc.
- La première formule de Steiner-Minkowski est vraie pour C :
- Soit (Pn) une suite de polygones contenus dans C tel que la distance de Haudorff entre Pn et C soit inférieur à 1/n, et les périmètres et les aires de Pn et C diffèrent de moins de 1/n. Si on note ap l'aire de Pn et pp son périmètre, on dispose des majorations :
- On dispose ensuite des majorations, si a désigne l'aire de C :
- On en déduit :
- Il suffit alors de faire tendre n vers plus l'infini pour conclure.
- La deuxième formule de Steiner-Minkowski est vraie pour C :
- C'est une conséquence directe de la première formule de Minkowski et du fait que le coefficient de degré 1 est égal au périmètre de la frontière.
Dimension quelconque
Énoncé de la formule
Soit , et un ensemble compact. Soit la mesure de Lebesgue (volume) de . On définit la quantité par la formule suivante (formule de Minkowski-Steiner):
avec
désignant la boule fermée de rayon , et
est la somme de Minkowski de et , d'où
Remarques
Mesure de la surface
Pour un ensemble "suffisamment irrégulier" , la quantité ne correspond pas nécessairement à la mesure -dimensionnelle du bord de . Voir Federer (1969) pour un traitement complet de ce problème.
Ensembles convexes
Quand l'ensemble est convexe, la limite inférieure ci-dessus est une vraie limite et on peut montrer
où est une fonction continue sur et désigne la mesure (ou volume) de la boulé unité de :
avec désignant la fonction gamma.
Exemple : volume et surface d'une boule
Prenons qui donne la formule de l'aire de la sphère de rayon , :
avec défini ci-dessus.
Références
Sources
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Minkowski-Steiner formula » (voir la liste des auteurs).
- (en) Bernard Dacorogna, Introduction to the Calculus of Variations, Londres, Imperial College Press, , 228 p., poche (ISBN 978-1-86094-508-3, LCCN 2004056946, lire en ligne)
- (en) Herbert Federer, Geometric Measure Theory, New-York, Springer-Verlag,
 Portail des mathématiques
Portail des mathématiques



































![{\displaystyle =\lim _{\delta \to 0}{\frac {[(R+\delta )^{n}-R^{n}]\omega _{n}}{\delta }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf2dab443dccfcaa5e285f5476539fe9f5c54406)













