Suite de Kolakoski

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

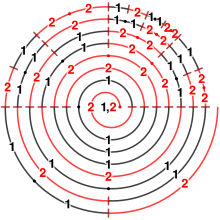
En mathématiques, la suite de Kolakoski, proposée et étudiée par William Kolakoski (en) en 1965^[1]^,^[2], est une suite autoréférente infinie de symboles 1 et 2 qui est son propre codage par plages^[3].

Définition

Les premiers termes de la suite sont :

1,2,2,1,1,2,1,2,2,1,2,2,1,1,2,1,1,2,2,1,2,1,1,2,1,2,2,1,1, ... (suite A000002 de l'OEIS)

Chaque symbole apparaît dans une « plage » d'un ou deux termes consécutifs et si l'on regroupe les termes par plages de 1 et de 2 :

(1),(2,2),(1,1),(2),(1),(2,2),(1),...,

la suite formée des longueurs successives de ces plages redonne la suite de départ : 1,2,2,1,1,2,1,... ; c'est la seule suite à deux symboles 1 et 2 ayant cette propriété et commençant par un 1^[3]^,^[4].

Propriétés

Il est raisonnable de penser que la densité asymptotique de chaque symbole est 1/2, mais cette conjecture reste non démontrée^[5]. Václav Chvátal a montré que la densité supérieure des 1 est inférieure à 0,50084 en 1993^[6] et le meilleur résultat dans cette direction est une borne de 0,50008^[7].

Il est remarquable que pour l'unique suite infinie de symboles 1 et 3 débutant à 1 et qui est son propre codage par plages, qui a pour premiers termes : 1, 3, 3, 3, 1, 1, 1, 3, 3, 3, 1, 3, 1, 3, 3, 3,... , on sait calculer exactement la fréquence du chiffre 3 (égale environ à 0,6) ; voir la suite A064353 de l'OEIS.

La suite de Kolakoski a également été remarquée par des informaticiens. Ainsi, Stephen Wolfram la décrit en relation avec l'étude des systèmes de tague cycliques^[8]^,^[9].

Remplaçant les 1 par des 0, les 2 par des 1, on peut interpréter la suite comme le développement d'un réel en base 2 ; ce réel est parfois encore appelé constante de Kolakoski^[10].

Notes et références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kolakoski sequence » (voir la liste des auteurs).

↑ (en) William Kolakoski, « Self-generating runs, Problem 5304 », Am. Math. Monthly, vol. 72,‎ 1965, p. 674 ; pour une solution partielle, voir (en) Necdet Üçoluk, « Self Generating Runs », Am. Math. Monthly, vol. 73,‎ 1966, p. 681-682.
↑ Cependant, cette suite était déjà apparue dès 1939 dans (en) Rufus Oldenburger, « Exponent trajectories in symbolic dynamics », Trans. Amer. Math. Soc., vol. 46,‎ 1939, p. 453-466 (JSTOR 1989933).
↑ ^{a et b} (en) N. Pytheas Fogg, Valérie Berthé (éditeur), Sébastien Ferenczi (éditeur), Christian Mauduit (éditeur) et A. Siegel (éditeur), Substitutions in dynamics, arithmetics and combinatorics, Berlin, Springer-Verlag, coll. « Lecture Notes in Mathematics », 2002 (1^re éd. 1794), 402 p. (ISBN 3-540-44141-7, zbMATH 1014.11015), p. 93.
↑ Plus précisément, on associe à la suite $u_{n}$ (formée de 1 et de 2) la suite $v_{n}$ qui compte la longueur des plages de $u_{n}$ (autrement dit, si $v_{n}=1$ correspond à la plage $u_{N}=2$ , mettons, c'est que $u_{N-1}=u_{N+1}=1$ , de même, si $v_{n}=2$ correspond à la plage $u_{N}=u_{N+1}=2$ , c'est que $u_{N-1}=u_{N+2}=1$ , et dans tous les cas, $v_{n+1}$ correspondra à la plage suivante, débutant à $u_{N+1}$ ou $u_{N+2}$ respectivement. La suite de Kolakoski est la seule suite pour laquelle les deux suites $u_{n}$ et $v_{n}$ sont identiques.
↑ Integer Sequences and Arrays.
↑ (en) Vašek Chvátal, Notes on the Kolakoski Sequence, DIMACS Technical Report 93-84, décembre 1993.
↑ M. Rao, « Trucs et bidules sur la séquence de Kolakoski », 2012.
↑ Ainsi nommés en référence au jeu du loup, tag game en anglais.
↑ A New Kind of Science, p. 895.
↑ Voir la suite A118270 de l'OEIS.

Voir aussi

Bibliographie

(en) Jean-Paul Allouche et Jeffrey Shallit, Automatic Sequences : Theory, Applications, Generalizations, Cambridge University Press, 2003, 571 p. (ISBN 978-0-521-82332-6, zbMATH 1086.11015, lire en ligne), p. 337
(en) F. M. Dekking, « What is the long range order in the Kolakoski sequence? », dans R. V. Moody, Proceedings of the NATO Advanced Study Institute (Waterloo, 1995), Dordrecht, Netherlands, Kluwer, 1997, p. 115-125
(en) J. M. Fédou et G. Fici, « Some remarks on differentiable sequences and recursivity », J. Integer Sequ., vol. 13, n^o 3, 2010, article 10.3.2
(en) Abdallah Hammam, « Some New Formulas for the Kolakoski sequence A000002 », Turkish Journal of Analysis and Number Theory, vol. 4 , n^o 3, 2016, p. 54-59, lire en ligne DOI 10.12691/tjant-4-3-1
(en) M. S. Keane (de), « Ergodic theory and subshifts of finite type », dans T. Bedford et M. Keane, Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Oxford, England, Oxford University Press, 1991, p. 35-70
(en) J. C. Lagarias, « Number theory and dynamical systems », dans S. A. Burr (en), The Unreasonable Effectiveness of Number Theory, Providence, RI, AMS, 1992, p. 35-72.
(en) G. Paun (en) et A. Salomaa, « Self-reading sequences », Am. Math. Monthly, vol. 103, 1996, p.166-168
(en) Jeffrey Shallit, « Number theory and formal languages », dans Dennis A. Hejhal, Joel Friedman, Martin C. Gutzwiller et Andrew M. Odlyzko, Emerging Applications of Number Theory, Springer-Verlag, coll. « The IMA Volumes in Mathematics and its Applications » (n^o 109), 1999 (ISBN 0-387-98824-6, lire en ligne), p. 547-570
(en) Bertran Steinsky, « A recursive formula for the Kolakoski sequence A000002 », J. Integer Sequ., vol. 9, 2006, article 06.3.7