Determináns (matematika)

Ez a szócikk a matematikai determinánsról szól. Hasonló címmel lásd még: Determináns (nyelvészet).

A determináns egy négyzetes mátrixokhoz rendelt szám. Hozzárendelésének tulajdonságait a mátrixok alaptestének tulajdonságai határozzák meg. A vegyes szorzat általánosítása magasabb dimenziókra. Multivektorok pszeudoskalár komponense, amely az elemi térfogat nagyságát és irányítását adja meg.

Legyen ${\displaystyle T}$ test, ${\displaystyle A\in T^{n\times n}}$ négyzetes mátrix és ${\displaystyle det:T^{n\times n}\rightarrow T}$ függvény. A mátrix determinánsának nevezzük ${\displaystyle det(A)}$-t, ha a hozzárendelést az alábbi négy axióma írja le:

1. homogén,	azaz:	${\displaystyle \det {\begin{pmatrix}\dots &\lambda _{i}a_{i}&\dots \end{pmatrix}}=\lambda _{i}\det {\begin{pmatrix}\dots &a_{i}&\dots \end{pmatrix}};}$
2. additív,		${\displaystyle \det {\begin{pmatrix}\dots &a_{i}+b_{i}&\dots \end{pmatrix}}=\det {\begin{pmatrix}\dots &a_{i}&\dots \end{pmatrix}}+\det {\begin{pmatrix}\dots &b_{i}&\dots \end{pmatrix}};}$
3. alternáló,		${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}&\dots \end{pmatrix}}=-\det {\begin{pmatrix}\dots &a_{j}&\dots &a_{i}&\dots \end{pmatrix}};}$
4. az egységmátrix determinánsa 1,		${\displaystyle \det {\begin{pmatrix}e_{1}&e_{2}&\dots &e_{n}\end{pmatrix}}=1.}$

Ahol:

• ${\displaystyle \lambda _{i}\in T}$ skalár, ${\displaystyle a_{i},b_{i}\in T^{n}}$ a mátrix oszlopait leíró vektor,
• ${\displaystyle \lambda _{i}a_{i},a_{i}+b_{i}}$ rendre a ${\displaystyle T^{n}}$ vektortéren definiált skalárral való szorzás és additív művelet,
• ${\displaystyle e_{i}={\begin{pmatrix}0&\dots &1_{i}&\dots &0\end{pmatrix}}^{T}}$ az ${\displaystyle i}$-edik egységvektor/bázis.

A leképezés a mátrix oszlopvektorain értelmezett n-változós függvényként értelmezhető (${\displaystyle V^{n}\rightarrow T}$). Az első kettő axiómával egy multilineáris, a harmadikkal egy antiszimmetrikus forma/funkcionál.

Az axiómák egyértelműen meghatározzák a leképezést. Egy másik ${\displaystyle T^{n\times n}\rightarrow T}$ függvény, amely kielégíti a fenti négy tulajdonságot azonos ${\displaystyle \det()}$-tel. Más megfogalmazásban az adott szabályokkal tetszőleges mátrixhoz egyértelmű értéket tudunk rendelni.

A harmadik axióma helyett állhatna az is, hogy két tetszőleges oszlopot megcserélve a determináns ${\displaystyle -1}$-szeresére változik. Az ${\displaystyle i}$-edik és ${\displaystyle j}$-edik oszlop cseréje ${\displaystyle 2|i-j|-1}$ darab szomszédos oszlopcserével elérhető és ${\displaystyle (-1)^{2|i-j|-1}=-1}$.

${\displaystyle A\in T^{n\times n}}$ esetén n-ed rendű determinánsról beszélünk. Az esetek többségében ${\displaystyle T}$ a valós (${\displaystyle \mathbb {R} }$) vagy komplex (${\displaystyle \mathbb {C} }$) számok halmaza.

Legyen ${\displaystyle T}$ test, ${\displaystyle A\in T^{n\times n}}$ négyzetes mátrix és ${\displaystyle det:T^{n\times n}\rightarrow T}$ függvény. A mátrix determinánsának nevezzük ${\displaystyle det(A)}$-t, ha a hozzárendelést az alábbi formula írja le:

${\displaystyle \det(A)=\sum _{\sigma }{(-1)^{I(\sigma )}\prod _{i=1}^{n}{a_{i\sigma _{i}}}}}$.

Ahol:

• ${\displaystyle a_{ij}}$ a mátrix ${\displaystyle i}$-edik sorában és ${\displaystyle j}$-edik oszlopában lévő elem,
• ${\displaystyle \sigma }$ (szigma) az ${\displaystyle (1,2,\dots ,n)}$ elemek egy permutációja,
• ${\displaystyle I(\sigma )}$ a permutáció inverziószáma.

A determinánsra adott két definíció ekvivalens.

A produktum a mátrix minden sorából és oszlopából kiemel pontosan egy elemet és n-tényezős szorzatokat alkot. A szumma megfelelő előjellel összegzi az összes lehetséges n-tényezős szorzatot. A képzett összeg tagszáma n faktoriálissal egyenlő.

Az inverziószám hivatott kifejezni, hogy a permutáció minimálisan hány cserére van az eredeti sorrendtől. Ha egy adott sorrend páratlan cserével elérhető, akkor párossal nem, és fordítva.

Az inverziószámmal történő hatványozás helyett a Levi-Civita-szimbólum segítségével is felírható a formula, mely lényegében ugyanazt fejezi ki.

Egy ${\displaystyle A\in T^{n\times k}}$ mátrix egyes sorainak és oszlopainak a törlésével kapott ${\displaystyle m\times m}$-es négyzetes mátrix determinánsát az ${\displaystyle A}$ egy m-ed rendű aldeterminánsának nevezzük.

Egy ${\displaystyle A\in T^{n\times n}}$ négyzetes mátrix ${\displaystyle i}$-edik sorának és ${\displaystyle j}$-edik oszlopának a törlésével kapott ${\displaystyle (n-1)\times (n-1)}$-es négyzetes mátrix determinánsát az ${\displaystyle A}$ mátrix ${\displaystyle a_{ij}}$ eleméhez tartozó aldeterminánsának nevezzük. Elemhez tartozó mátrix jelölése: ${\displaystyle A_{ij}}$.

Egy ${\displaystyle A\in T^{n\times k}}$ mátrix néhány sorának és oszlopának levágásával kapott ${\displaystyle m\times m}$-es négyzetes mátrix determinánsát az ${\displaystyle A}$ egy m-ed rendű sarokdeterminánsának nevezzük. Bal felső sarokdetermináns, jobb alsó sarokdetermináns, stb.

A determináns néhány szokásos jelölése:

• a mátrix megadásával: ${\displaystyle \det(A)}$, ${\displaystyle |A|}$;
• vektorrendszerrel: ${\displaystyle \det(a_{1},a_{2},\dots ,a_{n})}$;
• mátrix oszlopvektoraival: ${\displaystyle \det {\begin{pmatrix}a_{1}&a_{2}&\dots &a_{n}\end{pmatrix}}}$;
• a mátrixelemek megadásával: ${\displaystyle \det {\begin{pmatrix}a_{11}&a_{12}&\dots &a_{1n}\\\vdots &&&\vdots \\a_{n1}&a_{n2}&\dots &a_{nn}\end{pmatrix}}}$, illetve ${\displaystyle {\begin{vmatrix}a_{11}&a_{12}&\dots &a_{1n}\\\vdots &&&\vdots \\a_{n1}&a_{n2}&\dots &a_{nn}\end{vmatrix}}}$.

1. Ha két oszlop megegyezik, akkor a determináns ${\displaystyle 0}$.

3. axióma: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{i}&\dots \end{pmatrix}}=-\det {\begin{pmatrix}\dots &a_{i}&\dots &a_{i}&\dots \end{pmatrix}}}$.

${\displaystyle 2\det {\begin{pmatrix}\dots &a_{i}&\dots &a_{i}&\dots \end{pmatrix}}=0}$.

${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{i}&\dots \end{pmatrix}}=0}$.

2. Nem változik a determináns, ha az egyik oszlopból egy másik oszlop skalárral vett szorzatát levonjuk/hozzáadjuk.

2. axióma: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}+\lambda a_{i}&\dots \end{pmatrix}}=\det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}&\dots \end{pmatrix}}+\det {\begin{pmatrix}\dots &a_{i}&\dots \lambda a_{i}&\dots \end{pmatrix}}}$.

1. axióma: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}+\lambda a_{i}&\dots \end{pmatrix}}=\det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}&\dots \end{pmatrix}}+\lambda \det {\begin{pmatrix}\dots &a_{i}&\dots a_{i}&\dots \end{pmatrix}}}$.

1. tétel: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}+\lambda a_{i}&\dots \end{pmatrix}}=\det {\begin{pmatrix}\dots &a_{i}&\dots &a_{j}&\dots \end{pmatrix}}+0}$.

3. Ha az egyik oszlop a nullvektor, akkor a determináns is ${\displaystyle 0}$.

2.tétel: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &0&\dots \end{pmatrix}}=\det {\begin{pmatrix}\dots &a_{i}&\dots &0+1a_{i}&\dots \end{pmatrix}}}$.

1.tétel: ${\displaystyle \det {\begin{pmatrix}\dots &a_{i}&\dots &0&\dots \end{pmatrix}}=0}$.

4. Egy oszlop nem nulla skalárral való szorzása, két oszlop felcserélése és egyik oszlophoz egy másik oszlop skalárral való szorzatának hozzáadása nem változtat a determináns nulla voltán.

1. axióma: nem nulla skalár kiemelése a determinánst nem nullával szorozza.

3. axióma: két oszlop felcserélése a determinánst ${\displaystyle -1}$-gyel szorozza.

2. tétel: nem változik a determináns, ha egyik oszlophoz egy másik oszlop skalárral való szorzatát adjuk.

5. A determináns akkor és csak akkor ${\displaystyle 0}$, ha a vektorok lineárisan összefüggőek.

• Ha lineárisan összefüggő akkor ${\displaystyle 0}$:

Összefüggőség: ${\displaystyle 0=\sum _{i=1}^{n}{\lambda _{i}a_{i}}\rightarrow \exists \lambda _{j}\neq 0\rightarrow a_{j}=\sum _{i=1,i\neq j}^{n}{-{\frac {\lambda _{i}}{\lambda _{j}}}a_{i}}}$.

2. tétel: ${\displaystyle \det(a_{1}\dots a_{j}\dots a_{n})=\det(a_{1}\dots \sum _{i=1,i\neq j}^{n}{-{\frac {\lambda _{i}}{\lambda _{j}}}a_{i}}\dots a_{n})=\det(a_{1}\dots 0\dots a_{n})}$.

3. tétel: ${\displaystyle \det(a_{1}\dots 0\dots a_{n})=0}$.

• Ha lineárisan független, akkor nem ${\displaystyle 0}$:

Függetlenség: A mátrix tetszőleges oszlopában biztosan található egy nem nulla elem. Ellenkező esetben az oszlopvektorok lineárisan összefüggenének. Legyen ez az ${\displaystyle a_{ij}}$.

4. és 10. tétel: A ${\displaystyle j}$-edik oszlopból kiemeljük az ${\displaystyle a_{ij}}$-t, azaz az oszlopot megszorozzuk az ${\displaystyle a_{ij}}$ reciprokával. Az új ${\displaystyle a_{ij}=1}$. Lenullázzuk a ${\displaystyle i}$-edik sor, majd a ${\displaystyle j}$-edik oszlop minden ${\displaystyle a_{ij}}$-tól különböző elemét. Kicseréljük a ${\displaystyle j}$-ediket az ${\displaystyle i}$-edik oszlopra, ezzel létrehozva az ${\displaystyle e_{i}}$ egységvektort a megfelelő helyen. Az átalakítás nem változtat a vektorok lineáris függetlenségén és a már meglévő egységvektorokon. Az algoritmust az összes további oszlopra elvégezve kialakítható az egységmátrix, s a determináns a nem nulla kiemelt skalárok szorzata lesz.

6. Kifejtési tétel

${\displaystyle \det(A)=\sum _{j=1}^{n}{(-1)^{i+j}a_{ij}A_{ij}}}$.

A bizonyítás kulcsa az ${\displaystyle a_{j}}$ oszlopvektor ${\displaystyle \sum _{i=1}^{n}{a_{ij}e_{i}}}$ alakban történő felírása, majd az axiómák alkalmazása.

7. Ferde kifejtési tétel

${\displaystyle \det(A)=\sum _{j=1,i\neq k}^{n}{(-1)^{i+j}a_{ij}A_{kj}}=0}$.

1. tétel: Egy adott sor szerinti kifejtésnél másik sorhoz tartozó aldeterminánsokat használva azt a látszatot keltjük, mintha a mátrix ${\displaystyle i}$-edik és ${\displaystyle k}$-adik sora megegyezne.

8. Sarrus-szabály

9. A determinánsra adott két definíció ekvivalens.

• 6. tétel: Az ${\displaystyle A\in T^{n\times n}}$ mátrix determinánsa n-tagú összegként írható fel, amely eggyel kisebb rendű determinánsokból áll. A képletben az összes determinánst bontsuk újabb összegekre, és így tovább. Addig, míg mindegyik ${\displaystyle \det(a_{ij})}$ alakú nem lesz, melynek értéke már triviálisan az ${\displaystyle a_{ij}}$. Összesen ${\displaystyle n-1}$ lépcsőben kell végrehajtani a kifejtési tételt. Így egy olyan összeget kapunk, amelynek összes tagja az ${\displaystyle a_{1\sigma _{1}},a_{2\sigma _{2}},\dots ,a_{n\sigma _{n}}}$ elemek egy produktuma valamilyen előjellel, ahol ${\displaystyle (\sigma _{1},\sigma _{2},\dots ,\sigma _{n})}$ az ${\displaystyle (1,2,\dots ,n)}$ elemek egy permutációja. Az összes lehetséges permutációhoz tartozó szorzat pontosan egyszer szerepel az előjeles összegzésben:

${\displaystyle \det(A)=\sum _{\sigma }{p_{\sigma }\prod _{i=1}^{n}{a_{i\sigma _{i}}}}}$.

3.axióma: Cseréljük meg az ${\displaystyle a_{1\sigma _{1}}\dots a_{i\sigma _{i}}a_{(i+1)\sigma _{i+1}}\dots a_{n\sigma _{n}}}$ szorzatokban ugyanazt a két egymás melletti tagot. A csere az iterált kifejtés szemszögéből úgy tűnik, hogy egy olyan mátrixnak határozzuk meg a determinánsát, melyben a ${\displaystyle i}$-edik és ${\displaystyle i+1}$-edik sorok fel vannak cserélve. Az axióma miatt a teljes összeg, s benne a szorzatok előjelet váltanak. Ez összhangban van az elemek permutációjával, s a tagok előjelét az inverziószám paritása adja meg:

${\displaystyle p_{\sigma }=(-1)^{I(\sigma )}}$.

• A Leibniz-formulából könnyedén igazolhatóak az axiómák mint a formula elemi tulajdonságai.

10. ${\displaystyle \det(A)=\det(A^{T})}$.

A Leibniz-formula alakjából következik, hogy nincs semmi különbség sor és oszlop között, mikor a determináns meghatározása a cél. Ennek következménye, hogy az axiomatikus definícióban említett átalakítások és az oszlopokra kimondott tételek sorokra is ugyanúgy érvényesek.

11. ${\displaystyle \det(AB)=\det(A)\det(B)}$,

a determinánsok szorzástétele.

12. ${\displaystyle \det(A^{-1})={\frac {1}{\det(A)}}}$.

11.tétel: ${\displaystyle \det(A)\det(A^{-1})=\det(AA^{-1})=\det(E)=1}$.

Következmény: Ha egy mátrixnak 0 a determinánsa, akkor nem invertálható.

13. ${\displaystyle \det(\alpha A)=\alpha ^{n}\det(A)}$.

14. Hasonló mátrixok determinánsa egyenlő.

${\displaystyle \det(A)=\det(B^{-1}A^{*}B)=\det(B^{-1})\det(A^{*})\det(B)=\det(A^{*})}$.

15. Ha egy négyzetes mátrixnak van n darab sajátértéke, akkor ${\displaystyle \det(A)=\prod _{1}^{n}{\lambda _{i}}}$.

Ha megengedjük a komplex értékeket valós mátrix esetén, a sajátértékek szorzata továbbra is valós marad és ugyanúgy a determinánst adják meg.

16. ${\displaystyle abc=\det {\begin{pmatrix}a,b,c\end{pmatrix}}}$,

a vegyes szorzat és a determináns kapcsolata.

A determináns abszolút értéke:

Az n db n-dimenziós oszlop- vagy sorvektor által kifeszített n-dimenziós paralelepipedon n-dimenziós térfogatát adja meg.

• 2×2-es esetben a vektorok által kifeszített paralelogramma területét,
• 3×3-as esetben a vektorok által kifeszített paralelepipedon térfogatát.

A determináns előjele:

Az n db n-dimenziós vektorból álló vektorrendszer (rendezett vektor n-es) irányítását/sodrását adja meg.

• Pozitív esetben a vektorok pozitív irányítású/jobbsodrású rendszert alkotnak.
• Negatív esetben a vektorok negatív irányítású/balsodrású rendszert alkotnak.
• Nulla esetén nem értelmezzük az irányítást/sodrást.

Irányítás jelentése:

Szemléletesen megadja a választ, hogy beforgathatóak-e a vektorrendszer tagjai a kanonikus bázis vektorainak irányába úgy, hogy az elsőt az elsőhöz, i-ediket az i-edikez, stb. forgatjuk, miközben egyik vektor útja sem keresztezheti a többi által kifeszített alteret.

Ezen feltételek mellett n-dimenzióban n-1 darab vektor mindig összeforgatható, amelyek olyan alteret feszítenek ki, hogy az n-dimenziós teret két részre osztják. Az n. vektor pedig vagy az egyikben vagy a másikban található, így a beforgatása során vagy át kell lépni az alteret vagy sem. Emiatt minden nem nulla dimenzióban két összeforgathatósági osztály létezik. A bázis egyedül azt jelöli ki, melyik osztály tagjait tekintjük pozitív irányítású ill. jobb sodrású rendszereknek. A két osztály egymás tükörképe.

A fentiekből adódik, hogy n-dimenzióban n-nél kisebb dimenziós alteret kifeszítő vektorrendszer irányítása nem értelmezhető. Nem azonos elemszámú vektorrendszerek párosítása értelmetlen és n darab lineárisan összefüggő vektor a forgatástól függően a bázissal összeforgatható is, meg nem is.

Oszlopok átalakításának értelmezése a térfogat szemszögéből:

1. axióma: ha a paralelepipedon egyik oldalának hosszát ${\displaystyle \lambda }$-szorosára nyújtjuk, akkor térfogata ${\displaystyle \left|\lambda \right|}$-szeresére nő.

2. axióma: ha a paralelepipedont ketté szeljük (egyik oldalával párhuzamosan), akkor a térfogata a szeletek térfogatának (előjeles) összege.

3. axióma: a paralelepipedon térfogatának nagysága független az őt leíró vektorok sorrendjétől.

4. axióma: az n-dimenziós egységkocka térfogata ${\displaystyle 1}$.

Sorok átalakításának értelmezése a térfogat szemszögéből:

1. axióma: ha az egyik bázist ${\displaystyle \lambda }$-szorosára nyújtjuk, akkor ${\displaystyle \left|\lambda \right|}$-szeresére nyújtjuk a teret, s benne a test térfogatát.

3. axióma: a paralelepipedon térfogatának nagysága független attól, hogy az i-edik koordináták melyik sorban szerepelnek.

4. axióma: az n-dimenziós egységkocka térfogata ${\displaystyle 1}$.

Oszlopok átalakításának értelmezése az irányítás szemszögéből:

1. axióma: egy vektort ellentétes irányúra változtatva ellentétes irányításúvá válik a rendszer.

3. axióma: vektorok sorrendjének cseréje ellentétes irányításúvá teszi a rendszert.

4. axióma: a bázist az adott sorrenddel pozitív irányításúnak tekintjük.

Sorok átalakításának értelmezése az irányítás szemszögéből:

1. axióma: egyik bázis irányát ellentétesre változtatva az irányításba való besorolás felcserélődik.

3. axióma: két bázisvektor sorrendjének megcserélése miatt az irányításba való besorolás felcserélődik.

4. axióma: a bázis jelöli ki, melyek a pozitív irányítású rendszerek.

Tételek értelmezése:

1. tétel: Elfajuló paralelepipedon esetén egyes élek egy egyenesbe esnek. Ekkor a test lapos, térfogata 0.

2. tétel: A test éleivel/oldalaival/alapjával való párhuzamos nyírás nem változtat a térfogaton/magasságon és a körüljáráson.

3. tétel: Ha a test egyik éle 0 hosszúságú, térfogata is 0.

4. tétel: Az említett átalakítások megőrzik a kifeszített test dimenzióját és az alteret, amelyben fekszik.

A mátrix rangja adja meg a lineárisan független oszlopvektorok maximális számát, amely egyenlő a kifeszített test, ill. altér dimenziójával. Tehát az átalakítások nem változtatják meg a mátrix rangját. Ezeket a mátrix elemi átalakításainak nevezzük.

5. tétel: Lineárisan összefüggő vektorrendszer n-nél kisebb dimenziós testet feszít ki, melynek n-dimenziós térfogata 0.

A maximális, el nem tűnő aldetermináns rendje adja meg egy mátrix rangját, azaz a kifeszített test pontos dimenzióját. Négyzetes mátrix determinánsa önmagának aldeterminánsa, így értéke meghatározza a rangot.

A mátrixok lineáris leképezést írnak le. A mátrix oszlopai az egységkocka leképezés általi képének éleit adja meg. Négyzetes mátrix esetén a determináns nagysága fejezi ki, hogy hányszorosára nyújtja az elemi cellák térfogatát a leképezés. A determináns előjele pedig megadja, hogy egy lineárisan független vektorrendszer képének irányítása hogyan változik meg az eredetihez képest:

• pozitív: változatlan lesz az irányítása;
• negatív: irányítása ellentétes lesz;
• nulla: vektorrendszer képe összefüggő lesz, melynek így nincs irányítása.

A hasonló mátrixok ugyan azt a lineáris leképezést írják le, csak másik bázisban. Tehát egy lineáris leképezésnek több mátrixreprezentációja létezik. A mátrix a bázissal együtt teljes. Továbbá, négyzetes hasonló mátrixok determinánsa megegyezik. Ez a tény feljogosít arra, hogy egy lineáris leképezés determinánsáról beszéljünk. Általánosan a hasonló mátrixok közös tulajdonságai automatikusan az általuk reprezentált lineáris leképezés tulajdonságai is. Így beszélhetünk egy lineáris leképezés rangjáról, normájáról, nyomáról, sajátértékeiről, sajátvektorairól, karakterisztikus polinomjáról, stb. A matematika nyelvén ezt úgy mondjuk, hogy ezen tulajdonságok a bázistranszformációkkal szemben invariánsak.

Az azonos rendű négyzetes mátrixok szorzása asszociatív és egységelemes, azonban nem minden mátrixnak akad inverze. Az inverzzel rendelkező mátrixok halmaza azonos a nem nulla determinánssal rendelkező négyzetes mátrixok halmazával. A szorzástétel értelmében pedig ez a halmaz zárt a szorzás műveletére.

Az invertálható mátrixok a mátrixszorzás műveletével csoportot alkotnak. A mátrixok által reprezentált transzformációk csoportját általános lineáris csoportnak nevezzük. Jelölése: ${\displaystyle GL(n)}$.

A ${\displaystyle \pm 1}$ determinánssal rendelkező mátrixok a fenti csoport részcsoportját alkotják. Jele: ${\displaystyle O(n)}$. Részhalmaza az ortogonális mátrixok csoportja, amelyek az origó fixpontú távolságtartó és szögtartó transzformációkat írják le (forgatás és tükrözés).

Ezenfelül részcsoportját képezi a ${\displaystyle +1}$ determinánsú terület- és irányításmegőrző mátrixok halmaza, a speciális lineáris csoport. Jele: ${\displaystyle SO(n)}$. Részhalmaza a ${\displaystyle +1}$ determinánsú ortogonális mátrixok csoportja, amelyek a folytonosan kivitelezhető távolságtartó és szögtartó transzformációkat írják le (forgatás). (A tükrözés megtöri a folytonosságot.)

• Vegyes szorzat

A vegyes szorzat három 3-dimenziós vektor által kifeszített paralelepipedon térfogatának nagyságát adja meg. Előjele jobb sodrású rendszer esetén pozitív, bal sodrású esetén negatív. Akkor és csak akkor 0, ha a vektorok egy síkba vagy egy egyenesbe esnek. Ezek alapján egyértelmű, hogy a determináns ennek a kiterjesztése tetszőleges dimenzióra.

• Hiperdetermináns

Itt alapvetően a mátrixok általánosítása történik meg többdimenziós számtömbökké, s a determináns fogalma követi a kiterjesztést.

• Gyűrűk feletti determináns

A Leibniz-formula alapján a determináns meghatározásához nem kell a multiplikatív művelet invertálhatósága. Ez a tény a fogalom általánosabb bevezetését teszi lehetővé gyűrűk felett, mint például az egész számok vagy polinomok gyűrűje.

A multivektor a vektor fogalmának egyik irányú általánosítása. Több vektor együtteséből önálló matematikai objektumot alkotva definiáljuk a k-vektorokat, azaz az egyszerű multivektorokat, amelyek a vektorok által kifeszített ponthalmazt jellemzik. Tetszőleges multivektor pedig ezek lineáris kombinációja, azaz nem minden lineáris kombináció k-vektor.

A felépítésükben az ún. ékszorzat segít (${\displaystyle a_{1}\wedge ...\wedge a_{k}}$). Az ékszorzás egy kétváltozós művelet, amely asszociatív, antikommutatív és bilineáris (az összeadásra vonatkoztatva). Az antikommutativitás miatt ${\displaystyle e_{i}\wedge e_{i}=0}$. A bilinearitás miatt pedig a multivektorok bázisa az ${\displaystyle 1;e_{1},e_{2},...,e_{n};e_{1}\wedge e_{2},e_{1}\wedge e_{3},e_{2}\wedge e_{3},...;...;e_{1}\wedge ...\wedge e_{n}}$.

Egy k-vektor bázisbeli együtthatói az őt előállító k darab vektor k-dimenziós alterekbe eső komponensei által alkotott vektorrendszer determinánsa. Érthetőbben fogalmazva az együtthatók a k darab vektor által alkotott ${\displaystyle n\times k}$-s mátrix k-ad rendű aldeterminánsai. Példa:

${\displaystyle {\begin{array}{l}a\wedge b=(a_{1}e_{1}+a_{2}e_{2}+a_{3}e_{3}+a_{4}e_{4})\wedge (b_{1}e_{1}+b_{2}e_{2}+b_{3}e_{3}+b_{4}e_{4})\end{array}}}$

${\displaystyle {\begin{array}{l}a\wedge b=&&a_{1}b_{1}e_{1}\wedge e_{1}&+&a_{1}b_{2}e_{1}\wedge e_{2}&+&a_{1}b_{3}e_{1}\wedge e_{3}&+&a_{1}b_{4}e_{1}\wedge e_{4}\\&+&a_{2}b_{1}e_{2}\wedge e_{1}&+&a_{2}b_{2}e_{2}\wedge e_{2}&+&a_{2}b_{3}e_{2}\wedge e_{3}&+&a_{2}b_{4}e_{2}\wedge e_{4}\\&+&a_{3}b_{1}e_{3}\wedge e_{1}&+&a_{3}b_{2}e_{3}\wedge e_{2}&+&a_{3}b_{3}e_{3}\wedge e_{3}&+&a_{3}b_{4}e_{3}\wedge e_{4}\\&+&a_{4}b_{1}e_{4}\wedge e_{1}&+&a_{4}b_{2}e_{4}\wedge e_{2}&+&a_{4}b_{3}e_{4}\wedge e_{3}&+&a_{4}b_{4}e_{4}\wedge e_{4}\\\\a\wedge b=&&0&+&a_{1}b_{2}e_{1}\wedge e_{2}&+&a_{1}b_{3}e_{1}\wedge e_{3}&+&a_{1}b_{4}e_{1}\wedge e_{4}\\&-&a_{2}b_{1}e_{1}\wedge e_{2}&+&0&+&a_{2}b_{3}e_{2}\wedge e_{3}&+&a_{2}b_{4}e_{2}\wedge e_{4}\\&-&a_{3}b_{1}e_{1}\wedge e_{3}&-&a_{3}b_{2}e_{2}\wedge e_{3}&+&0&+&a_{3}b_{4}e_{3}\wedge e_{4}\\&-&a_{4}b_{1}e_{1}\wedge e_{4}&-&a_{4}b_{2}e_{2}\wedge e_{4}&-&a_{4}b_{3}e_{3}\wedge e_{4}&+&0\\\end{array}}}$

${\displaystyle {\begin{array}{l}a\wedge b=&&(a_{1}b_{2}-a_{2}b_{1})e_{1}\wedge e_{2}&+&(a_{1}b_{3}-a_{3}b_{1})e_{1}\wedge e_{3}&+&(a_{1}b_{4}-a_{4}b_{1})e_{1}\wedge e_{4}&&\\&+&(a_{2}b_{3}-a_{3}b_{2})e_{2}\wedge e_{3}&+&(a_{2}b_{4}-a_{4}b_{2})e_{2}\wedge e_{4}&+&(a_{3}b_{4}-a_{4}b_{3})e_{3}\wedge e_{4}&&\\\\\|a\wedge b\|^{2}=&&(a_{1}b_{2}-a_{2}b_{1})^{2}&+&(a_{1}b_{3}-a_{3}b_{1})^{2}&+&(a_{1}b_{4}-a_{4}b_{1})^{2}&&\\&+&(a_{2}b_{3}-a_{3}b_{2})^{2}&+&(a_{2}b_{4}-a_{4}b_{2})^{2}&+&(a_{3}b_{4}-a_{4}b_{3})^{2}&&\\\end{array}}}$

A k-vektor normája az őt ékszorzással előállító k darab vektor által leírt paralelepipedon k-dimenziós térfogatának a nagysága.

Az egyszerű multivektorok típusai:

• 0-argumentumú ékszorzat eredménye a 0-vektor, a skalár megfelelője;
• 1-argumentumú ékszorzat eredménye az 1-vektor, a vektor megfelelője;
• n-1 darab n-dimenziós vektor ékszorzata a pszeudovektor, együtthatói az általánosított vektoriális szorzat eredménye;
• n darab n-dimenziós vektor ékszorzata a pszeudoskalár, együtthatója a vektorok alkotta négyzetes mátrix determinánsa;
• n-nél több n-dimenziós vektor ékszorzata 0.

• Paralelepipedon térfogata

${\displaystyle V={\sqrt {\det \left(A^{T}A\right)}}}$

A k-dimenziós test k-dimenziós térfogata n-dimenzióban. Az ${\displaystyle A\in T^{n\times k}}$ mátrix oszlopai a testet kifeszítő vektorokból áll.

• Cramer-szabály

${\displaystyle x_{i}={\frac {\det {\begin{pmatrix}...&a_{i-1}&b&a_{i+1}&...\end{pmatrix}}}{\det(A)}}}$

Invertálható mátrixú lineáris egyenletrendszernek egyértelműen létezik megoldása. A képlettel elkerülhetjük a teljes megoldás kiszámítását, ha csak egy részmegoldásra van szükségünk.

• Vektoriális szorzat 3 dimenzióban

${\displaystyle a\times b={\begin{vmatrix}i&j&k\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}}}$

• Vektoriális szorzat általánosan

${\displaystyle \operatorname {cross} (a_{1},...,a_{n-1})={\begin{vmatrix}a_{11}&\cdots &a_{1(n-1)}&e_{1}\\\vdots &\ddots &\vdots &\vdots \\a_{n1}&\cdots &a_{n(n-1)}&e_{n}\\\end{vmatrix}}=(-1)^{n+1}{\begin{vmatrix}e_{1}&\cdots &e_{n}\\a_{11}&\cdots &a_{n1}\\\vdots &\ddots &\vdots \\a_{1(n-1)}&\cdots &a_{n(n-1)}\\\end{vmatrix}}}$

A bázisvektorok alkotják az n. oszlop elemeit. Ez szokatlan lehet elsőre, de formailag a szorzás eredményét adja vissza. A bázist tartalmazó oszlopra/sorra alkalmazzuk a kifejtési tételt. Az eredmény koordinátáit a bázisokhoz mint elemekhez tartozó előjeles aldeterminánsok szolgáltatják. Oszlopcserékkel és transzponálással a megszokott alakban is felírható.

• Helyettesítéses integrálás

${\displaystyle \int _{g(U)}F=\int _{U}F\circ g\left|\operatorname {J} _{g}\right|}$

A függvény alatti területet n-dimenziós tégla alapú hasábok térfogatával közelítjük. Pontosabban ezen közelítések határértékeként definiáljuk. Parametrizáció esetén ezen közelítő hasábok alapja deformálódik, a térfogatuk megváltozik, ezért korrekcióra van szükség. Meg kell határoznunk, hogy a paramétertartományban elhelyezkedő n-dimenziós egységkocka adott pont körüli képe milyen a paraméterezett tartományon. A képet a parametrizáció állítja elő. A leképezés adott pontbeli tulajdonságát a derivált, azaz a Jacobi-mátrix jellemzi. A Jacobi-mátrix oszlopvektorai (a paramétervonalak érintői) írják le a deformált egységkocka éleit, melynek irányított térfogata a mátrix determinánsa.

• Mátrix inverze

${\displaystyle A^{-1}={\frac {\operatorname {adj} A^{T}}{\det A}}}$

Nem csak az eredeti mátrix determinánsára van szükségünk. Egy mátrix adjungáltjának előállításához szükségünk van még az elemekhez tartozó aldeterminánsokra is: ${\displaystyle \operatorname {adj} A=((-1)^{i+j}A_{ij})}$. (A formula bizonyításához a kifejtési és a ferde kifejtési tétel szükséges.)

• Sajátvektor és sajátérték

${\displaystyle \det(A-\lambda E)=0}$

A determináns eredménye ${\displaystyle \lambda }$ n-ed fokú polinomja, a mátrix karakterisztikus függvénye. A polinom gyökei szolgáltatják a sajátértékeket. A Viète-formulákból következik, hogy a mátrix nyoma, ${\displaystyle tr(A)=-a_{n-1}/a_{n}}$ és determinánsa, ${\displaystyle det(A)=(-1)^{n}a_{0}/a_{n}}$. Valós mátrixok polinomja valós, melyek nem minden esetben bonthatóak fel elsőfokú tényezők szorzatára. Ez magyarázat arra, miért nincs mindig n db (valós) sajátértéke a mátrixnak. Különlegesek a komplex értékű mátrixok, mert az algebra alaptétele szerint mindig van n db komplex gyöke egy komplex polinomnak, így n db sajátértéke, és sajátvektora a komplex mátrixnak.

• Alacsony rendű mátrixok

1×1-es mátrix determinánsa maga a szám: ${\displaystyle {\begin{vmatrix}a_{11}\end{vmatrix}}=a_{11}}$.

2×2-es mátrix determinánsa: ${\displaystyle {\begin{vmatrix}a&b\\c&d\end{vmatrix}}=ad-bc}$.

• Elemi átalakítások

A determináns az axiomatikus definíció által biztosított négy szabállyal meghatározható. Cél az egységmátrix kialakítása. Felhasznált tételek a 2. és 10. tétel. Két kimenetele van:

1. Sikerül előállítani az egységmátrixot, melynek már ismert a determinánsa (${\displaystyle =1\Leftarrow }$ 4. axióma).
2. Kialakítunk egy nullvektort vagy sorban vagy oszlopban, mely mátrixnak szintén ismert a determinánsa (${\displaystyle =0\Leftarrow }$ 3. tétel).

Paraméteresen levezetni az eredményt nehéz és csak elbonyolítja a feladatot. Konkrét számításoknál alkalmazható jól.

Első példa:

${\displaystyle {\begin{vmatrix}2&4&0&-2\\4&12&3&5\\-8&-14&0&0\\5&11&1&0\end{vmatrix}}=2{\begin{vmatrix}1&4&0&-2\\2&12&3&5\\-4&-14&0&0\\5/2&11&1&0\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\2&4&3&9\\-4&2&0&-8\\5/2&1&1&5\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\0&4&3&9\\0&2&0&-8\\0&1&1&5\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\0&1&3&0\\0&2&0&-8\\0&0&1&2\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&2&-6&-8\\0&0&1&2\end{vmatrix}}=}$

${\displaystyle 2{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&-6&-8\\0&0&1&2\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&-6&4\\0&0&1&0\end{vmatrix}}=2{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&0&4\\0&0&1&0\end{vmatrix}}=8{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&0&1\\0&0&1&0\end{vmatrix}}=-8{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{vmatrix}}=-8}$

Második példa:

${\displaystyle {\begin{vmatrix}1&9&9&5\\1&2&2&5\\0&{\sqrt {2}}&\pi &x\\0&0&lg(3)&0\end{vmatrix}}=lg(3){\begin{vmatrix}1&9&9&5\\1&2&2&5\\0&{\sqrt {2}}&\pi &x\\0&0&1&0\end{vmatrix}}=lg(3){\begin{vmatrix}1&9&0&5\\1&2&0&5\\0&{\sqrt {2}}&0&x\\0&0&1&0\end{vmatrix}}=lg(3){\begin{vmatrix}1&9&0&0\\1&2&0&0\\0&{\sqrt {2}}&0&x\\0&0&1&0\end{vmatrix}}=lg(3)\cdot x{\begin{vmatrix}1&9&0&0\\1&2&0&0\\0&{\sqrt {2}}&0&1\\0&0&1&0\end{vmatrix}}=}$

${\displaystyle lg(3)\cdot x{\begin{vmatrix}1&9&0&0\\1&2&0&0\\0&0&0&1\\0&0&1&0\end{vmatrix}}=lg(3)\cdot x{\begin{vmatrix}0&7&0&0\\1&2&0&0\\0&0&0&1\\0&0&1&0\end{vmatrix}}=7\cdot lg(3)\cdot x{\begin{vmatrix}0&1&0&0\\1&0&0&0\\0&0&0&1\\0&0&1&0\end{vmatrix}}=-7\cdot lg(3)\cdot x{\begin{vmatrix}0&1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\end{vmatrix}}=7\cdot lg(3)\cdot x{\begin{vmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{vmatrix}}=7\cdot lg(3)\cdot x}$

Meghatározhatóak a következőek is:

Rang: Az átalakítás során a megjelenő nullvektorokkal nem foglalkozunk és addig alakítjuk tovább a mátrixot, amíg minden sor/oszlop vagy lenullázódik vagy megjelenik benne egy bázisvektor. Egy teljes vagy hiányos egységmátrix kialakítása a cél. A bázisok száma adja meg a mátrix rangját. (Nem kvadratikus mátrixok esetén is így kell.)

${\displaystyle \operatorname {rg} {\begin{pmatrix}-2&-6&-4\\-2&-10&-2\\1&1&3\\3&1&10\end{pmatrix}}=\operatorname {rg} {\begin{pmatrix}1&3&2\\-2&-10&-2\\1&1&3\\3&1&10\end{pmatrix}}=\operatorname {rg} {\begin{pmatrix}1&3&2\\0&-4&2\\0&-2&1\\0&-8&4\end{pmatrix}}=\operatorname {rg} {\begin{pmatrix}1&0&0\\0&-4&2\\0&-2&1\\0&-8&4\end{pmatrix}}=\operatorname {rg} {\begin{pmatrix}1&0&0\\0&0&2\\0&0&1\\0&0&4\end{pmatrix}}=\operatorname {rg} {\begin{pmatrix}1&0&0\\0&0&0\\0&0&1\\0&0&0\end{pmatrix}}=2}$

Inverz mátrix: A determináns meghatározásakor az egységmátrix eljutásáig alkalmazott lépéseket ugyanabban a sorrendben alkalmazva az egységmátrixon az eredeti mátrix inverz mátrixát kapjuk. (Nulla determináns esetén nem tudunk eljutni az egységmátrixhoz.)

${\displaystyle {\begin{array}{c}A=&{\begin{pmatrix}2&4\\1&3\end{pmatrix}}&\rightarrow &{\begin{pmatrix}1&2\\1&3\end{pmatrix}}&\rightarrow &{\begin{pmatrix}1&2\\0&1\end{pmatrix}}&\rightarrow &{\begin{pmatrix}1&0\\0&1\end{pmatrix}}&\\&{\begin{pmatrix}1&0\\0&1\end{pmatrix}}&\rightarrow &{\begin{pmatrix}1/2&0\\0&1\end{pmatrix}}&\rightarrow &{\begin{pmatrix}1/2&0\\-1/2&1\end{pmatrix}}&\rightarrow &{\begin{pmatrix}3/2&-2\\-1/2&1\end{pmatrix}}&=A^{-1}\end{array}}}$

• Kifejtési tétel

A determinánst egyik sorához/oszlopához tartozó előjeles aldeterminánsaira vezetjük vissza. A módszer iterálása a Leibniz-formulához vezet. Segédmódszere, hogy minél több 0-t tartalmazó sort/oszlopot válasszunk, így kevesebb tagú összeget kell felírni.

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}&=a\,{\begin{vmatrix}\Box &\Box &\Box \\\Box &e&f\\\Box &h&i\end{vmatrix}}-b\,{\begin{vmatrix}\Box &\Box &\Box \\d&\Box &f\\g&\Box &i\end{vmatrix}}+c\,{\begin{vmatrix}\Box &\Box &\Box \\d&e&\Box \\g&h&\Box \end{vmatrix}}\\[3pt]&=a\,{\begin{vmatrix}e&f\\h&i\end{vmatrix}}-b\,{\begin{vmatrix}d&f\\g&i\end{vmatrix}}+c\,{\begin{vmatrix}d&e\\g&h\end{vmatrix}}\\[3pt]&=aei+bfg+cdh-ceg-bdi-afh.\end{aligned}}}$

• Sarrus-szabály

Felhívja a figyelmet egy geometriai mintázatra, így kevesebb számítás szükséges a determinánshoz. Csak 3×3-as mátrixnál alkalmazható, ill. 3×3-as aldetermináns meghatározásánál. Leibniz-formula 3×3-as mátrixra vonatkozó esete.

${\displaystyle {\begin{aligned}|A|={\begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}}=\end{aligned}}}$ ${\displaystyle =\color {red}{afj+bgh+cei}\color {blue}{-hfc-iga-jeb}}$

• Leibniz-formula

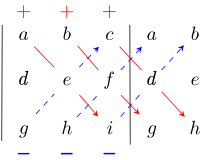
Elméleti jelentősége a determináns paraméteres leírásából adódik. Gyakorlati szempontból a determináns eme definíciója nehezen kezelhető, hiszen bár 2×2-re és 3×3-ra léteznek egyszerű kiszámítási módok, a magasabb rendűekre még nem találtak ilyet. A definícióból történő kiszámítás már ${\displaystyle n=4}$-re is ${\displaystyle 24}$ tagot eredményez, ${\displaystyle n=6}$ esetben pedig már ${\displaystyle 720}$-at, ugyanis a szumma tagszáma ${\displaystyle n!}$.

• Gauss-elimináció

Háromszögmátrix, diagonális mátrix determinánsa a főátlóban lévő elemek szorzata. Nem trianguláris mátrixból a determináns változását szem előtt tartva Gauss-eliminációval mindig kialakíthatunk egy ilyen mátrixot. Ez tekinthető az elemi módszer speciális esetének.

${\displaystyle {\begin{vmatrix}a_{11}&a_{12}&\dots &a_{1n}&\\0&a_{11}&&&\\\vdots &&&\vdots &\\0&0&\dots &a_{nn}&\end{vmatrix}}=\prod _{i=1}^{n}{a_{ii}}}$

• LU felbontás

A 4×4-esnél nagyobb mátrix esetén a mechanikus kiszámítás túl sok művelettel jár, ezért az ún. LU felbontást használják. A módszer a determinánsok szorzástételére és a háromszögmátrixokra épül.

• 2×2

Kifejtési tétel/Leibniz-formula következtében:

${\displaystyle {\begin{vmatrix}2&5\\3&1\end{vmatrix}}=2\cdot 1-5\cdot 3=-13}$

A ${\displaystyle (2,5)}$ és a ${\displaystyle (3,1)}$ vektorok által leírt paralelogramma területének nagysága 13 egység. A vektorok balsodrású rendszert alkotnak 2-dimenzióban.

• 3×3

Gauss-eliminációval háromszögmátrix kialakítása:

${\displaystyle {\begin{vmatrix}2&0&10\\-2&6&-4\\3&10&17\end{vmatrix}}={\begin{vmatrix}2&0&10\\0&6&6\\0&10&2\end{vmatrix}}=6\cdot {\begin{vmatrix}2&0&10\\0&1&1\\0&10&2\end{vmatrix}}=6\cdot {\begin{vmatrix}2&0&10\\0&1&1\\0&0&-8\end{vmatrix}}=6\cdot 2\cdot 1\cdot -8=-96}$

• 4×4

Ebben az esetén hatékony eljárás a kifejtési tétel alkalmazása a mátrix valamelyik sorára vagy oszlopára, majd a tétel további alkalmazása helyett a Sarrus-szabály alapján számoljuk ki az aldeterminánsokat. A példában a mátrix első sora szerint történik a kifejtés:

${\displaystyle {\begin{vmatrix}1&2&3&4\\5&6&7&8\\9&10&11&12\\13&14&15&16\\\end{vmatrix}}=(-1)^{1+1}\cdot 1\cdot {\begin{vmatrix}6&7&8\\10&11&12\\14&15&16\\\end{vmatrix}}+(-1)^{1+2}\cdot 2\cdot {\begin{vmatrix}5&7&8\\9&11&12\\13&15&16\\\end{vmatrix}}+(-1)^{1+3}\cdot 3\cdot {\begin{vmatrix}5&6&8\\9&10&12\\13&14&16\\\end{vmatrix}}+(-1)^{1+4}\cdot 4\cdot {\begin{vmatrix}5&6&7\\9&10&11\\13&14&15\\\end{vmatrix}}=}$

${\displaystyle =1\cdot 1\cdot 0-1\cdot 2\cdot 0+1\cdot 3\cdot 0-1\cdot 4\cdot 0=0}$

• A. G. Kuros: Felsőbb algebra, Tankönyvkiadó, Budapest, 1975
• Wettl Ferenc: Lineáris algebra