Matematikai inga

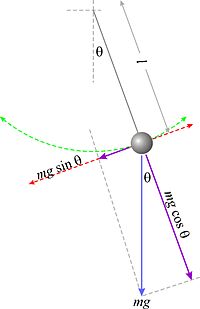
A matematikai inga egy elhanyagolható tömegű ${\displaystyle l}$ hosszúságú fonalra függesztett, ${\displaystyle m}$ tömegű pontszerű testből áll, amelyre szabad erőként csak a nehézségi erő hat. Az egyensúlyi helyzetéből kitérített inga csillapítatlan periodikus mozgást végez. Ennek az idealizált modellnek a gyakorlati megvalósítása egy vékony fonálra felfüggesztett fémgolyó (egy fonálinga), ami az egyensúlyi helyzetéből kitérítve, függőleges síkban egy körív mentén a két szélső helyzet között közelítőleg csillapítatlanul leng.^[1]

A matematikai inga mozgását a dinamika alapegyenletéből lehet meghatározni. A nehézségi erőn kívül hat még a fonálban ébredő erő (F), ami mindig a fonál irányában hat, azaz a mozgás során mindig sugárirányú. Ez a fonálerő és a nehézségi erőnek a sugárirányú komponense hozza létre a körpályán való mozgáshoz a centripetális erőt. Erre a következőt írhatjuk fel:

${\displaystyle F-mg\cos \theta =m{\frac {v^{2}}{l}}}$,

ahol: ${\displaystyle F}$ a fonálban ébredő erő, ${\displaystyle m}$ a test tömege, ${\displaystyle g}$ a földi nehézségi gyorsulás, ${\displaystyle \theta }$ a fonál függőlegessel bezárt szöge, ${\displaystyle l}$ a fonál hossza, ${\displaystyle v}$ a lengést végző tömegpont pillanatnyi sebessége.

A fonálban ébredő kényszererő nagysága a mozgás során tehát változik. Legnagyobb az értéke a pálya legalsó pontján, amikor a fonál függőleges, és a sebesség a legnagyobb. A szélső helyzetben a legkisebb.

A nehézségi erő érintő irányú komponense a körpálya menti gyorsulást hozza létre, és így meghatározza az inga helyzetét, a fonál függőlegessel bezárt szögét az idő függvényében. Erre a következőt írhatjuk fel:

${\displaystyle ma_{t}=-mg\sin \theta }$,

ahol ${\displaystyle a_{t}}$ az érintő (tangenciális) irányú gyorsulás.

A tangenciális gyorsulás és a szöggyorsulás (${\displaystyle \beta }$) kapcsolata:

${\displaystyle a_{t}=\beta l}$.

A szöggyorsulás a szögkitérés második deriváltja:

${\displaystyle \beta ={\frac {d^{2}\theta }{dt^{2}}}}$.

Így a szögkitérésre a következő másodrendű differenciálegyenletet kapjuk:

${\displaystyle ml{\frac {d^{2}\theta }{dt^{2}}}=-mg\sin \theta }$.

A tömeggel egyszerűsítve, átrendezés után:

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\sin \theta =0}$.

Kis kitérések esetén a szinuszfüggvényt közelíteni lehet magával a szöggel:

${\displaystyle \sin \theta \approx \theta }$.

Ezt a közelítést alkalmazva kapjuk:

${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}+{\frac {g}{l}}\theta =0}$.

Bevezetve a következő jelölést:

${\displaystyle \omega ={\sqrt {\frac {g}{l}}}}$,

az egyenlet a következő alakra hozható: ${\displaystyle {\frac {d^{2}\theta }{dt^{2}}}=-\omega ^{2}\theta }$.

Ez az egyenlet a harmonikus rezgőmozgást végző test mozgásegyenlete. A matematikai inga mozgása tehát kis kitéréseknél ${\displaystyle \omega }$ körfrekvenciájú harmonikus rezgőmozgásnak tekinthető. A lengés periódusideje:

${\displaystyle T={\frac {2\pi }{\omega }}=2\pi {\sqrt {\frac {l}{g}}}}$.

Az inga helyzetét leíró időfüggvény, a szögkitérés az időfüggvényében a következő alakú:

${\displaystyle \theta =\phi _{max}\sin(\omega t+\delta )}$,

ahol ${\displaystyle \phi _{max}}$ a szögelfordulás amplitúdója (a legszélső helyzethez tartozó szög) és ${\displaystyle \delta }$ a kezdőfázis (a kezdeti nulla időponthoz tartozó helyzetet jellemző szögkitérés). A ${\displaystyle \phi _{max}}$ szögre kitérített, majd magára hagyott inga esetében ${\displaystyle \delta =\pi /2}$, és így ${\displaystyle \theta =\phi _{max}\cos(\omega t)}$

Az inga mozgásának közelítő megoldásából látszik, hogy kis kitérési szögek esetén a lengések frekvenciája nem függ az inga tömegétől és a lengések amplitúdójától, csak az inga hosszától és a nehézségi gyorsulástól. A közelítés megfelelő (1%-os relatív hiba alatti), ha a kilengések 9,9 foknál kisebbek, és még elfogadható (maximum 2,5%-os bizonytalanságú), ha a kilengések maximum 15 fokosak.

1. ↑ Demény A., Erostyák J., Szabó G., Trócsányi Z.: Fizika I. Klasszikus mechanika, Nemzeti Tankönyvkiadó, 2005, ISBN 963195577X

• Interaktív inga
• Fizikakönyv.hu – Az inga