Variabili di Mandelstam

In fisica teorica le variabili di Mandelstam sono grandezze fisiche che rappresentano energia, impulso e angoli delle particelle in processi di scattering in un sistema Lorentz-invariante. Vengono usate nel caso di urti elastici tra due particelle.

Le variabili di Mandelstam ${\displaystyle s,t,u}$ sono definite come:

• ${\displaystyle s=(p_{1}+p_{2})^{2}=(p_{3}+p_{4})^{2}}$
• ${\displaystyle t=(p_{1}-p_{3})^{2}=(p_{2}-p_{4})^{2}}$
• ${\displaystyle u=(p_{1}-p_{4})^{2}=(p_{2}-p_{3})^{2}}$

dove p₁ e p₂ sono i quadri-impulsi delle particelle incidenti mentre p₃ e p₄ sono i quadri-impulsi delle particelle uscenti.

s rappresenta il quadrato dell'energia nel sistema del centro di massa ( ${\displaystyle E^{CM}=M_{inv}c^{2}}$, dove ${\displaystyle M_{inv}}$ indica la massa invariante del sistema ) e t il quadrato della quantità di impulso trasferito durante l'urto.

Le lettere ${\displaystyle s,t,u}$ possono essere anche usate per individuare processi in canale-s, canale-t e canale-u. Questi canali rappresentano differenti tipi di diagrammi di Feynman o differenti processi di scattering quando l'interazione comporta lo scambio di una particella intermedia che possiede un momento ${\displaystyle {\sqrt {s}},{\sqrt {t}},{\sqrt {u}}}$,

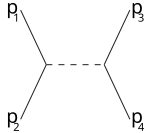
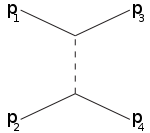
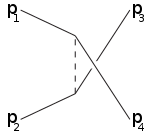
canale-s	canale-t	canale-u

Per esempio il canale-s corrisponde ad un processo in cui le particelle 1,2 interagiscono generando una particella intermedia, che infine decade nelle particelle 3 e 4: il canale-s è l'unico modo in cui si possono scoprire risonanze e nuove particelle instabili purché abbiano un tempo di vita sufficiente per essere rivelate.

Il canale-t rappresenta un processo in cui la particella 1 emette una particella intermedia e diventa la particella 3 dello stato finale, mentre la particelle 2 interagisce con la particella intermedia e diventa 4. Il canale-u è il canale-t nel quale si è scambiato il ruolo delle particelle 3 e 4.

Nel limite ultrarelativistico la massa può essere trascurata, quindi, ad esempio:

${\displaystyle s=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}\approx 2p_{1}\cdot p_{2}}$

dal momento che ${\displaystyle p_{1}^{2}=m_{1}^{2}}$ e ${\displaystyle p_{2}^{2}=m_{2}^{2}}$ (c =1).

In questo limite le variabili possono essere scritte come

${\displaystyle {\begin{aligned}s&\approx 2p_{1}\cdot p_{2}&\approx \quad \!2p_{3}\cdot p_{4}\\t&\approx -2p_{1}\cdot p_{3}&\approx -2p_{2}\cdot p_{4}\\u&\approx -2p_{1}\cdot p_{4}&\approx -2p_{3}\cdot p_{2}\\\end{aligned}}}$

Una proprietà di queste variabili è che la loro somma è pari alla somma dei quadrati delle masse delle particelle coinvolte (avendo posto c =1):

${\displaystyle s+t+u=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}}$.

Per la dimostrazione sono necessarie due considerazioni:

• il modulo quadro del quadri-impulso di una particella è il quadrato della sua massa,

${\displaystyle p_{i}^{2}=m_{i}^{2}\qquad \qquad \qquad \qquad \qquad \quad (1)}$

• e la conservazione del quadri-impulso,

${\displaystyle p_{1}=-p_{2}+p_{3}+p_{4}\qquad \qquad \qquad (2)}$

Si inizia scrivendo le tre variabili come:

${\displaystyle s=(p_{1}+p_{2})^{2}=p_{1}^{2}+p_{2}^{2}+2p_{1}\cdot p_{2}}$

${\displaystyle t=(p_{1}-p_{3})^{2}=p_{1}^{2}+p_{3}^{2}-2p_{1}\cdot p_{3}}$

${\displaystyle u=(p_{1}-p_{4})^{2}=p_{1}^{2}+p_{4}^{2}-2p_{1}\cdot p_{4}}$

usando la (1) si può scrivere:

${\displaystyle s=m_{1}^{2}+m_{2}^{2}+2p_{1}\cdot p_{2}}$

${\displaystyle t=m_{1}^{2}+m_{3}^{2}-2p_{1}\cdot p_{3}}$

${\displaystyle u=m_{1}^{2}+m_{4}^{2}-2p_{1}\cdot p_{4}}$

ora, sommando le tre equazioni si trova:

${\displaystyle {\begin{aligned}s+t+u&=3m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}+2p_{1}\cdot p_{2}-2p_{1}\cdot p_{3}-2p_{1}\cdot p_{4}\\&=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}+2\left(m_{1}^{2}+p_{1}\cdot p_{2}-p_{1}\cdot p_{3}-p_{1}\cdot p_{4}\right)\\&=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}+2\left(m_{1}^{2}+p_{1}\cdot \left(p_{2}-p_{3}-p_{4}\right)\right)\\\end{aligned}}}$

quindi, in conclusione:

${\displaystyle s+t+u=c^{2}(m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2})}$

• (EN) S. Mandelstam, Determination of the Pion-Nucleon Scattering Amplitude from Dispersion Relations and Unitarity, in Phys. Rev., vol. 112, n. 4, 1958, p. 1344, DOI:10.1103/PhysRev.112.1344. URL consultato il 22 maggio 2018 (archiviato dall'url originale il 28 maggio 2000).
• (EN) Francis Halzen e Alan Martin, Quarks & Leptons: An Introductory Course in Modern Particle Physics, John Wiley & Sons, 1984, ISBN 0-471-88741-2.
• (EN) Donald H. Perkins, Introduction to High Energy Physics, 4ª ed., Cambridge University Press, 2000, ISBN 0-521-62196-8.

• Diagramma di Feynman
• Stanley Mandelstam

Portale Fisica: accedi alle voci di Wikipedia che trattano di fisica