ホモクリニック軌道

数学において、ホモクリニック軌道(homoclinic orbit)とは、力学系における流れの軌跡で、鞍点（saddle point）から出て、同じ鞍点に戻ってくる軌道である。

より厳密に、鞍点での安定多様体と不安定多様体の積集合とも定義できる。 反復写像系（離散力学系）でも、ホモクリニック軌道や、ホモクリニックポイントは同様に、安定多様体と不安定多様体の不動点と周期点を用いて定義することができる。

次のような常微分方程式で定義された連続力学系を考える。

${\displaystyle {\dot {x}}=f(x)}$

${\displaystyle x=x_{0}}$が不動点であり、解${\displaystyle \phi (t)}$が次を満たすならばホモクリニック軌道である。

${\displaystyle \phi (t)\rightarrow x_{0}\quad \mathrm {as} \quad t\rightarrow \pm \infty }$

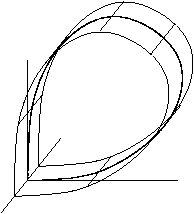
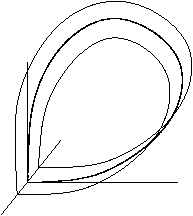
もし、相空間が3次元以上ならば、鞍点上の不安定多様体をより詳しく調べる必要がある。 大別して2つの場合について述べる。 一つ目は、不安定多様体が幾何学的には円筒型と同相である場合で、 二つ目は、不安定多様体が幾何学的には、メビウスの輪と同相である場合である。 二つ目のホモクリニック軌道を特に、ねじれていると呼ぶ。

離散力学系についても、ホモクリニック軌道は定義可能である。 写像${\displaystyle f:M\rightarrow M}$が、多様体${\displaystyle M}$の微分同相であるとき、 ${\displaystyle x}$が同じ未来と過去を持っている、つまりは、不動点または周期点${\displaystyle p}$が存在する

${\displaystyle \lim _{n\rightarrow \pm \infty }f^{n}(x)=p.}$

であるとき、${\displaystyle x}$をホモクリニックポイントと呼ぶ。

• John Guckenheimer and Philip Holmes, Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields (Applied Mathematical Sciences Vol. 42), Springer

• Homoclinic orbits in Henon map with Java applets and comments

• ヘテロクリニック軌道
• ホモクリニック分岐