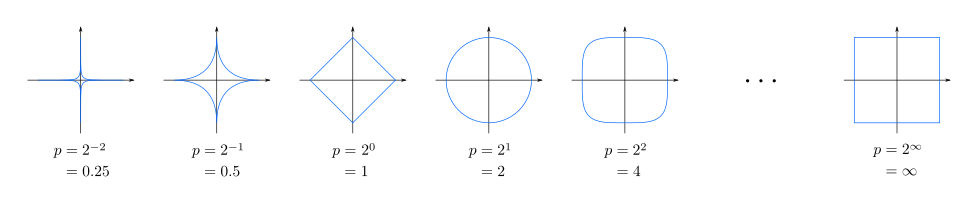ミンコフスキー距離とは、ノルム線型空間における距離計量で、ユークリッド距離およびマンハッタン距離を一般化したものと言える。ドイツの数学者ヘルマン・ミンコフスキーにちなんで名付けられた。
定義
ミンコフスキー距離の次数を「 (ただし、
(ただし、 は整数)」とした時、点
は整数)」とした時、点 と点
と点 (ただし、
(ただし、 および
および )の距離は、以下のように定義される。
)の距離は、以下のように定義される。

 の場合においては、ミンコフスキー距離はミンコフスキーの不等式の結果を満たす距離計量となる。もし
の場合においては、ミンコフスキー距離はミンコフスキーの不等式の結果を満たす距離計量となる。もし だった場合、点(0,0)と点(1,1)の間の距離は
だった場合、点(0,0)と点(1,1)の間の距離は となるが、双方の点と点(0,1)との間の距離は1となる。これは三角不等式に反するので、
となるが、双方の点と点(0,1)との間の距離は1となる。これは三角不等式に反するので、 の時は距離計量にはならない。しかし、このような距離計量は、単に
の時は距離計量にはならない。しかし、このような距離計量は、単に という冪指数を除去するだけで得られる。この距離計量は同時にF-ノルムでもある。
という冪指数を除去するだけで得られる。この距離計量は同時にF-ノルムでもある。
ミンコフスキー距離は通常、 が1または2の場合が用いられ、これはそれぞれマンハッタン距離とユークリッド距離に対応する。特殊な場合であるが、
が1または2の場合が用いられ、これはそれぞれマンハッタン距離とユークリッド距離に対応する。特殊な場合であるが、 が無限に発散する場合はチェビシェフ距離が得られる。
が無限に発散する場合はチェビシェフ距離が得られる。

同様に、 が負の無限大に発散する場合は、このような式になる。:
が負の無限大に発散する場合は、このような式になる。:

ミンコフスキー距離は、点Pと点Qの間の成分ごとの差の累乗平均の倍数と見なすこともできる。
以下の図は、 の値を様々に変化させた時の単位円(中心から等しい距離にある全ての点の集合)を示している。
の値を様々に変化させた時の単位円(中心から等しい距離にある全ての点の集合)を示している。
関連項目
External links
Simple IEEE 754 implementation in C++
NPM JavaScript Package/Module