相似の中心

幾何学において、相似の中心（そうじのちゅうしん、英: homothetic center, center of similarity, center of similitude）は、二つの図形が相似であるとき、その点を中心として拡大縮小（英語版）によって、一方の図形をもう一方の図形へ重ねることができる点である。 単に相似中心ともいう^[1][2][3][4]。相似の中心は、外相似点^[5]または外心^[6][7]（External center;相似外心^[8]）と、内相似点（Internal center; 相似内心）または内心に分けられる。外相似点での相似比は正、内相似点での相似比は負になる。

2つの図形が相似の中心を持つには、相似の中心において、対応する頂点との成す角が一致し、対応する点が同じ距離の比になければならない。2つの図形及びその相似の中心は、同一平面上にある必要はない。

任意の円はすべて相似である。一般の位置にあり、同半径でない二つの円には内側と外側の相似中心が存在する。二つの相似中心は2円の中心と共線（line of centers）である^[9]。点円（半径0の円）の円や虚円（半径が負の円）相似中心を定義できる。

与えられた2円について、様々な方法で相似中心を見つけることができる。解析幾何学の観点は、内相似点は重み付き平均（英語版）（重みはもう一方の円の半径）として定義できる。内相似点と円の中心との距離の比はもう一方の円の半径の比となる。それぞれ中心(x₁, y₁), (x₂, y₂)、半径r₁, r₂である円C₁, C₂の内相似点(x₀, y₀)は$${\displaystyle (x_{0},y_{0})={\frac {r_{2}}{r_{1}+r_{2}}}(x_{1},y_{1})+{\frac {r_{1}}{r_{1}+r_{2}}}(x_{2},y_{2}).}$$である。外相似点は同様の比で外分した点となる。$${\displaystyle (x_{e},y_{e})={\frac {-r_{2}}{r_{1}-r_{2}}}(x_{1},y_{1})+{\frac {r_{1}}{r_{1}-r_{2}}}(x_{2},y_{2}).}$$一般に、内分点は内相似点、外分点は外相似点に対応する。ただし、同半径の外相似点は、ユークリッド平面では0除算となり定義できない。射影平面では無限遠点に対応する。

総合幾何学においては2つの平行な直径を描き、端点を対応させて線分をそれぞれA₁B₁, A₂B₂とする。A₁A₂, B₁B₂の交点は外相似点、A₁B₂, B₁A₂の交点は内相似点になる。

限られた場合ではあるが、2円の共通接線が引ける場合、2つの共通内接線の交点は内相似点、2つの共通外接線の交点は外相似点となる^[10]。上の図でいえばA₁A₂, B₁B₂が共通接線となるときに当たる。

先述の様に、同半径の場合、共通外接線は平行になり、アフィン平面上では外相似点は存在しない。しかし射影平面では極限の場合として無限遠点になる。

異なる半径で、同心円である2円の相似中心は、双方その円の中心になる。同半径の場合も含めて、解析的手法でも、極限の場合でも、このことを確認できる。また、この場合 line of centersは存在せず、共通接線による構築もできない。

一方が点円でもう一方が実円の場合、2つの相似中心は点円と一致する。

2つの円が完全に一致する場合、内相似点は円の中心であるが外相似点は定義できない。正確に言えば母数空間で、外相似点を与える関数は、除去不能な不連続な点をもつ。同半径の2円を極限まで近づけた場合は、line of centers上の無限遠点になる。

異なる二つの点円に関しては、その外相似点はline of centers上の無限遠点となるが、内相似点は定義できない。

一般に、相似中心を通る直線はそれぞれの円と二点で交わる。これら四点において、二点が対応している（homologous; 相応、相当）とは、相似中心を通る直線とその点における半径が成す角が等しいときのことを指す^[11][12]。図4ではQ, Q'が対応する点となる。相似中心とは共線であるが、対応していない点を反相応（antihomologous; 反相当）という^[13][14]。図4ではQ, P'のことを指す^[13]。

同じ相似中心を通る2つの直線について、反相応な点は共円である。

図4の様に三角形△EQS, △EQ'S' を想定する。$${\displaystyle \angle QES=\angle Q'\!ES',\quad {\frac {\overline {EQ}}{\overline {EQ'}}}={\frac {\overline {ES}}{\overline {ES'}}},}$$であるから2つの三角形は相似である。相似の中心はEである。相似性より$${\displaystyle \angle ESQ=\angle ES'\!Q'=\alpha .}$$内接四角形の定理より$${\displaystyle \angle EP'\!R'=\angle ES'\!Q'.}$$ 四角形QSR'P'について、$${\displaystyle \angle QSR'=180^{\circ }-\alpha .}$$ であるからQSR'P'は円に内接する四角形である。方べきの定理より$${\displaystyle {\overline {EQ}}\cdot {\overline {EP'}}={\overline {ES}}\cdot {\overline {ER'}}.}$$同様にして四角形PRS'Q'が円に内接する事が示せるまた、^[1]$${\displaystyle {\overline {EP}}\cdot {\overline {EQ'}}={\overline {ER}}\cdot {\overline {ES'}}.}$$

内相似点Iに関しても同様に証明できる。$${\displaystyle {\begin{aligned}&\triangle PIR\cong \triangle P'\!IR'\\&\implies \angle RPI=\angle IP'\!R'=\alpha \\&\implies \angle RS'\!Q'=\angle PP'\!R'=\alpha \quad {\text{(inscribed angle theorem)}}\end{aligned}}}$$線分RQ'はPとS'において同じ角であるから円周角の定理（inscribed angle theorem）よりR, P, S', Q'の共円が従う。また、交弦定理から$${\displaystyle {\overline {IP}}\cdot {\overline {IQ'}}={\overline {IR}}\cdot {\overline {IS'}}.}$$同様に四角形QSP'R'の円の内接と次の式が示せる。$${\displaystyle {\overline {IQ}}\cdot {\overline {IP'}}={\overline {IS}}\cdot {\overline {IR'}}.}$$

2円の根軸とは、その直線上の点の二円への接線長が等しくなるような直線である。また、線上の点の2円への方べきが等しくなるような点とも定義される。根軸は line of centersと直交し、2円が交わる場合はその割線と一致する。3円について、2円に定義できるのべ3つの根軸は共点である。この点は根心と呼ばれる。根心の各円への接線長は等しい（根円を成す）。

任意の反相応する点は根軸を用いて見つけられる。図4の様に外相似点Eを通る2直線を作る。この2線がそれぞれ反相応な点Q, P'とS, R'で交わるとする。この4点は共円である。さらにその定義より直線QS,P'R'は新たな円と元の円の根軸になる。したがってQS,P'R'の交点Gは3円の根心である。

反相応点で、二つの円と接する円が存在する。逆に、2円に接する円の各接点は反相応である。

図5の様に2円の中心をO₁, O₂、外相似点をEとする。Eを通る直線により、円との交点P, Q, P',Q'を決める。O₁Q, O₂P' を延長して、その交点をT₁とすれば、T₁はQ, P'で各円と接する円になる。これは△O₁PQ, △O₂P'Q' の相似性と${\displaystyle {\overline {O_{1}P}}={\overline {O_{1}Q}}}$より$${\displaystyle \angle O_{1}PQ=\angle O_{1}QP=\angle O_{2}P'\!Q'=\angle O_{2}Q'\!P'=\angle T_{1}QP'=\angle T_{1}P'\!Q.}$$が成り立ち、△T₁P'Qが、T₁を頂角とする二等辺三角形、つまり$${\displaystyle {\overline {T_{1}P'}}={\overline {T_{1}Q}}.}$$であるからである。

他の反相応な点P, Q'で同様の性質が成り立つことも、内相似点に対して同様にして証明できる。

ある2円について、2円に接するすべての円の根心は同一であり。また2円の相似中心と一致する。図8のように、相似中心Eを通る2つの直線が与円と交わっているとし、その線上の反相応点を接点とする円T₁, T₂を書く。前項では、これら4つの接点が同一円周上にあることを示した。更に、T₁, T₂の根軸は相似中心Eを通る。

図5の様にすべての接点が共線であるとき、相似性より$${\displaystyle {\frac {\overline {EP}}{\overline {EP'}}}={\frac {\overline {EQ}}{\overline {EQ'}}};\quad {\overline {EP}}\cdot {\overline {EQ'}}={\overline {EQ}}\cdot {\overline {EP'}}.}$$このとき、Eにおける2つの接円に対する方べきが等しいことが分かるので、Eが根軸上にあることが分かる。

3円について、2円の組が3つできるので、相似中心は6つできる。特に6つのうち3つは共線である^[8]。

図9の様に3つの円が書かれた平面を用意する。3円の半径の比と同じ分、対応する中心から垂直に上に上がった点A',B',C'を書く。この3点のうち2点を通る直線と元の平面の交点をH_AB, H_BC, H_ACとする。 △H_ABAA', △H_ABBB' の相似からが分かる。$${\displaystyle {\frac {\overline {H\!_{AB}B}}{\overline {H\!_{AB}A}}}={\frac {r_{B}}{r_{A}}}}$$ ( r_A, r_B は円の半径)。したがってH_ABは2円の相似の中心である。同様にH_BCとH_ACも他の2円の相似中心であることが分かる。

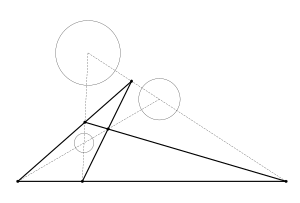
ここで、H_AB, H_BC, H_ACは元の面とA',B',C'を通る面の交線上にあるから、これを元の平面において見れば、H_AB, H_BC, H_ACの共線が示される。同様にして、他の相似中心の組においても共線が分かる。

C₁, C₂を与えられた3円に接する共役な円とする（図11）。ただしここで共役とは、2円が与円に対して同じ族にあることを意味する。前項の議論より2円に接する円のすべての根軸は2円の相似中心を通る。よって、与えられた3円の2円の組の相似中心の一つはC₁, C₂の根軸上に位置する。

この性質を活用して、ジェルゴンヌはアポロニウスの問題の一般解を求めた。3つの与円について、 解円の根軸は相似中心の共線にある。勿論、共軸な円は無数に存在するので、相似中心による議論のみでは、証明は完結しないことに注意する。

•  Johnson R.A『Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle』Dover Publications、1960年。 
• Kunkel, Paul (2007). “The tangency problem of Apollonius: three looks”. BSHM Bulletin: Journal of the British Society for the History of Mathematics 22 (1). doi:10.1080/17498430601148911. http://whistleralley.com/tangents/bshmkunkel.pdf. 

• 『相似変換』 - 高校数学の美しい物語