Identiti (matematik)

Dalam matematik, identiti ialah persamaan yang menghubungkan satu ungkapan matematik A kepada ungkapan matematik yang lain B, supaya A dan B (yang mungkin mengandungi beberapa pemboleh ubah) menghasilkan nilai yang sama untuk semua nilai pemboleh ubah dalam julat kesahan tertentu.^[1] Dengan kata lain, A = B ialah identiti jika A dan B mentakrifkan fungsi yang sama, dan identiti ialah kesamaan antara fungsi yang ditakrifkan secara berbeza. Sebagai contoh, ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ dan ${\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1}$ adalah identiti.^[1] Identiti kadangkala ditunjukkan oleh simbol bar ganda tiga, ≡ dan bukannya =, tanda sama dengan.^[2]

Identiti tertentu, seperti ${\displaystyle a+0=a}$ dan ${\displaystyle a+(-a)=0}$, membentuk asas algebra,^[3] manakala identiti lain, seperti ${\displaystyle (a+b)^{2}=a^{2}+2ab+b^{2}}$ dan ${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}$, boleh berguna dalam memudahkan ungkapan algebra dan mengembangkannya.^[4]

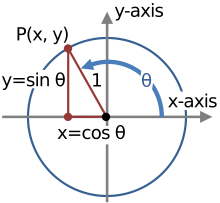
Secara geometri, identiti trigonometri ialah identiti yang melibatkan fungsi tertentu bagi satu atau lebih sudut.^[5] Ia berbeza daripada identiti segi tiga, iaitu identiti yang melibatkan kedua-dua sudut dan panjang sisi segi tiga. Hanya jenis pertama dibincangkan dalam rencana ini.

Identiti ini berguna apabila ungkapan yang melibatkan fungsi trigonometri perlu dipermudahkan. Satu lagi aplikasi penting ialah penyepaduan fungsi bukan trigonometri: teknik biasa yang melibatkan penggunaan peraturan penggantian dengan fungsi trigonometri dahulu, dan kemudian memudahkan kamiran yang terhasil dengan identiti trigonometri.

Salah satu contoh identiti trigonometri yang paling menonjol melibatkan persamaan ${\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}$ yang benar untuk semua nilai sebenar ${\displaystyle \theta }$. Sebaliknya, persamaan:

${\displaystyle \cos \theta =1}$

hanya benar untuk nilai tertentu ${\displaystyle \theta }$, tidak semua. Sebagai contoh, persamaan ini adalah benar apabila ${\displaystyle \theta =0,}$ tetapi palsu apabila ${\displaystyle \theta =2}$.

Satu lagi kumpulan identiti trigonometri melibatkan apa yang dipanggil formula penambahan/penolakan (contohnya identiti sudut dua ${\displaystyle \sin(2\theta )=2\sin \theta \cos \theta }$, formula penambahan untuk ${\displaystyle \tan(x+y)}$),^[2] yang boleh digunakan untuk memecahkan ungkapan sudut yang lebih besar kepada yang mempunyai juzuk yang lebih kecil.

Identiti berikut dipegang untuk semua eksponen integer, dengan syarat asasnya bukan sifar:

${\displaystyle {\begin{aligned}b^{m+n}&=b^{m}\cdot b^{n}\\(b^{m})^{n}&=b^{m\cdot n}\\(b\cdot c)^{n}&=b^{n}\cdot c^{n}\end{aligned}}}$

Tidak seperti penambahan dan pendaraban, eksponen tidak bersifat komutatif. Contohnya, 2 + 3 = 3 + 2 = 5 dan 2 · 3 = 3 · 2 = 6, tetapi 2³ = 8 manakala 3² = 9.

Di samping itu, eksponensi juga tidak bersekutu. Contohnya, (2 + 3) + 4 = 2 + (3 + 4) = 9 dan (2 · 3) · 4 = 2 · (3 · 4) = 24, tetapi 2³ darab 4 ialah 8⁴ (atau 4,096) manakala 2 darab 3 ⁴ ialah 2⁸¹ (atau 2,417,851,639,229,258,349,412,352). Apabila tiada tanda kurungan ditulis, mengikut konvensyen susunannya adalah atas ke bawah, bukan bawah ke atas:

${\displaystyle b^{p^{q}}:=b^{(p^{q})},}$ sedangkan ${\displaystyle (b^{p})^{q}=b^{p\cdot q}.}$

Beberapa formula penting, kadangkala dipanggil identiti logaritma atau peraturan log yang mengaitkan logaritma antara satu sama lain seperti di bawah.

Logaritma hasil darab ialah hasil tambah logaritma nombor yang didarab; logaritma nisbah dua nombor ialah perbezaan logaritma. Logaritma kuasa p bagi sesuatu nombor ialah p kali logaritma nombor itu sendiri; logaritma bagi punca p ialah logaritma nombor dibahagikan dengan p. Jadual berikut menyenaraikan identiti ini dengan contoh. Setiap satu identiti boleh diperolehi selepas penggantian definisi logaritma ${\displaystyle x=b^{\log _{b}x},}$ dan/atau ${\displaystyle y=b^{\log _{b}y},}$ di bahagian sebelah kiri.

	Formula	Contoh
Hasil darab	${\displaystyle \log _{b}(xy)=\log _{b}(x)+\log _{b}(y)}$	${\displaystyle \log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5}$
Hasil bahagi	${\displaystyle \log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)}$	${\displaystyle \log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4}$
Kuasa	${\displaystyle \log _{b}(x^{p})=p\log _{b}(x)}$	${\displaystyle \log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6}$
Punca kuasa	${\displaystyle \log _{b}\!{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}}$	${\displaystyle \log _{10}\!{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5}$

Log logaritma_b(x) boleh dikira daripada logaritma x dan b berkenaan dengan asas arbitrari k menggunakan formula berikut:

${\displaystyle \log _{b}(x)={\frac {\log _{k}(x)}{\log _{k}(b)}}.}$

Kalkulator saintifik lazim mengira logaritma berdasarkan asas 10 dan e.^[6] Logaritma berkenaan dengan sebarang asas b boleh ditentukan menggunakan salah satu daripada dua logaritma ini dengan formula sebelumnya:

${\displaystyle \log _{b}(x)={\frac {\log _{10}(x)}{\log _{10}(b)}}={\frac {\log _{e}(x)}{\log _{e}(b)}}.}$

Diberi nombor x dan log logaritmanya_b(x) kepada asas b yang tidak diketahui, asasnya diberikan oleh:

${\displaystyle b=x^{\frac {1}{\log _{b}(x)}}.}$

• Ensiklopedia Persamaan Ensiklopedia dalam talian identiti matematik (diarkibkan)
• Koleksi Identiti Algebra