Catalan-getal

In de combinatoriek vormen de Catalan-getallen een rij van natuurlijke getallen die voorkomen in diverse telproblemen. Ze zijn naar de Belgische wiskundige Eugène Catalan (1814–1894) genoemd.

Het ${\displaystyle n}$-de Catalan-getal wordt door de volgende formule met binomiaalcoëfficiënten gegeven

${\displaystyle C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}\qquad {\mbox{ voor }}n\geq 0.}$

De eerste Catalan-getallen^[1] zijn:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

Eigenschappen

Een alternatieve uitdrukking is

${\displaystyle C_{n}={2n \choose n}-{2n \choose n-1}\quad {\mbox{ voor }}n\geq 1.}$

Aan deze formule ziet men meteen dat ${\displaystyle C_{n}}$ een natuurlijk getal is, wat bij de eerder gegeven formule niet direct duidelijk is.

De Catalan-getallen voldoen ook aan de differentievergelijking:

${\displaystyle C_{0}=1\quad {\mbox{ en }}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}\,C_{n-i}\quad {\mbox{ voor }}n\geq 0.}$

Met de recursieve formule

${\displaystyle C_{0}=1\quad {\mbox{ en }}\quad C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n},}$

kunnen de Catalan-getallen efficiënt worden berekend.

De Catalan-getallen gedragen zich asymptotisch als

${\displaystyle C_{n}\sim {\frac {4^{n}}{n^{3/2}{\sqrt {\pi }}}}}$,

in de zin dat het quotiënt van beide leden in de limiet voor ${\displaystyle n\to \infty }$ naar 1 gaat.

De enige oneven Catalan-getallen^[2] zijn die met ${\displaystyle n=2^{k}-1}$; alle andere zijn even.

Toepassingen in combinatoriek

Allerlei telproblemen in de combinatoriek hebben Catalan-getallen als oplossingen. Hier zijn enkele voorbeelden, de meeste met illustratie van de gevallen ${\displaystyle C_{3}=5}$ en ${\displaystyle C_{4}=14.}$

• ${\displaystyle C_{n}}$ is het aantal correcte manieren om ${\displaystyle n}$ paren haakjes op te schrijven:

((()))     ()(())     ()()()     (())()     (()())

• ${\displaystyle C_{n}}$ is het aantal verschillende manieren waarop ${\displaystyle n+1}$ factoren compleet tussen haakjes kunnen worden gezet, zodanig dat er geen haakjes meer bij kunnen. Voor ${\displaystyle n=3}$, bijvoorbeeld, zijn er de volgende vijf manieren om de factoren van haakjes te voorzien:

${\displaystyle ((ab)c)d\quad (a(bc))d\quad (ab)(cd)\quad a((bc)d)\quad a(b(cd))}$

• Vergelijk het eerste voorbeeld met het aantal Dyck-woorden van lengte ${\displaystyle 2n}$. Een Dyck-woord is een string die alleen uit ${\displaystyle n}$ X-en en ${\displaystyle n}$ Y's bestaat, op zo'n manier dat geen enkel begindeel van de string meer Y's dan X-en heeft. Er zijn bijvoorbeeld de volgende Dyck-woorden van lengte 6:

XXXYYY     XYXXYY     XYXYXY     XXYYXY     XXYXYY.

• ${\displaystyle C_{n}}$ is het aantal binaire bomen vanuit één punt met ${\displaystyle n+1}$ bladeren:

• ${\displaystyle C_{n}}$ is het aantal paden in een rooster van ${\displaystyle n\times n}$ vierkante cellen die de punten linksonder en rechtsboven verbindt door alleen naar links en naar boven te gaan, zonder boven de diagonaal uit te komen. De volgende figuur laat het geval ${\displaystyle n=4}$ zien:

• ${\displaystyle C_{n}}$ is het aantal manieren waarop een convexe veelhoek met ${\displaystyle n+2}$ zijden in driehoeken langs de diagonalen kan worden verdeeld. De figuur toont het geval ${\displaystyle n=3}$:

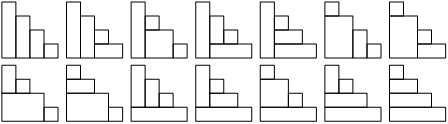
• ${\displaystyle C_{n}}$ is het aantal manieren waarop een trapvorm van hoogte ${\displaystyle n}$ met ${\displaystyle n}$ rechthoeken kan worden betegeld. De figuur toont het geval ${\displaystyle n=4}$.

Hankel-matrix

De ${\displaystyle n\times n}$-Hankel-matrix ${\displaystyle H_{n}}$ met als elementen ${\displaystyle H_{n}(i,j)=C_{i+j}}$, heeft determinant 1, onafhankelijk van de waarde van ${\displaystyle n}$. Voor ${\displaystyle n=4}$ bijvoorbeeld is

${\displaystyle \det {\begin{bmatrix}1&1&2&5\\1&2&5&14\\2&5&14&42\\5&14&42&132\end{bmatrix}}=1.}$

Merk op dat ook als de elementen worden "verschoven", zodat ${\displaystyle H_{n}(i,j)=C_{i+j+1}}$, de determinant dan nog steeds gelijk aan 1 is, onafhankelijk van de waarde van ${\displaystyle n}$. Voor ${\displaystyle n=4}$ bijvoorbeeld is

${\displaystyle \det {\begin{bmatrix}1&2&5&14\\2&5&14&42\\5&14&42&132\\14&42&132&429\end{bmatrix}}=1.}$

Geschiedenis

De rij van Catalan-getallen werd voor het eerst beschreven in 1751 in een brief aan Goldbach door Leonhard Euler, ^[3] die geïnteresseerd was in het verdelen van een veelhoek in driehoeken. De rij werd later naar Eugène Charles Catalan genoemd, die het verband met de uitdrukkingen met haakjes ontdekte, toen hij aan de Torens van Hanoi werkte. Johann Andreas von Segner vond in 1758 een recursieve formule, ^[4] waarvan Euler in de samenvatting bij Segner artikel de oplossing vermeldt. ^[5] Een door Johann Friedrich Pfaff opgestelde algemenere aftellingsmethode werd in 1795 door Nikolaus Fuß bewezen. ^[6] In de jaren 1838 en 1839 pakten Gabriel Lamé, ^[7] Olinde Rodrigues, ^[8] Jacques Binet ^{[9] [10]} en Eugène Catalan ^{[11] [12]} het probleem opnieuw op. Eugen Netto schreef in zijn in 1901 gepubliceerde leerboek over de combinatoriek de getallen aan Catalan toe. ^[13]