Termodynamisk beta

I statistisk termodynamikk er termodynamisk beta, også kjent som kulde, resiprok av den termodynamiske temperaturen til et system:

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$^[1]

Hvor:

${\displaystyle T}$ er temperaturen

${\displaystyle k_{B}}$ er Boltzmanns konstant

Den ble opprinnelig introdusert i 1971 (som Kältefunktion "kaldhetsfunksjon") av Ingo Müller, en av forkjemperne for den rasjonelle tankegang,^[2] basert på tidligere forslag om en "gjensidig temperatur" -funksjon.^[3][4]

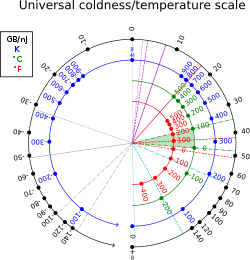
Termodynamisk beta har enheter resiprok med energien (i SI-enhet, resiprokjoule, ${\displaystyle [\beta ]={\textrm {J}}^{-1}}$). I ikke-termiske enheter kan den også måles i byte per joule, eller mer praktisk, gigabyte per nanojoule;^[5] 1 K⁻¹ tilsvarer omtrent 13 062 gigabyte per nanojoule; i romtemperatur: T = 300K, β ≈ 44 GB/nJ ≈ 39 eV⁻¹ ≈ 2,4×10²⁰ J⁻¹. Konverteringsfaktoren er 1 GB/nJ = ${\displaystyle 8\ln 2\times 10^{18}}$ J⁻¹.

Termodynamisk beta er egentlig forbindelsen mellom informasjonsteorien og statistisk mekanikkfortolkning av et fysisk system gjennom dets entropi og termodynamikken knyttet til energien. Det uttrykker entropiens respons på en økning i energi. Hvis et system utfordres med en liten mengde energi, beskriver β mengden systemet vil randomisere.

Via den statistiske definisjonen av temperatur som en funksjon av entropi, kan kuldefunksjonen beregnes i det mikrokanoniske ensemblet fra formelen

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(dvs. delvis derivat av entropien S med hensyn til energien E ved konstant volum V og partikkelnummer N).

Selv om β er fullstendig ekvivalent i konseptuelt innhold med temperatur, anses β generelt som en mer grunnleggende mengde enn temperatur på grunn av fenomenet negativ temperatur, der β er kontinuerlig når den krysser null, mens T har en egenart.^[6]

I tillegg har β fordelen av å være lettere å forstå årsaksvis: Hvis en liten mengde varme tilsettes et system, er β økningen i entropi delt på økningen i varme. Temperatur er vanskelig å tolke i samme forstand, da det ikke er mulig å "legge til entropi" til et system bortsett fra indirekte, ved å modifisere andre størrelser som temperatur, volum eller antall partikler.

Fra et statistisk synspunkt er β en numerisk størrelse som relaterer to makroskopiske systemer i likevekt. Den eksakte formuleringen er som følger. Tenk på to systemer, 1 og 2, i termokontakt, med respektive energier E₁ og E₂. Vi antar at E₁ + E₂ =konstant E. Antall mikrotilstander i hvert system vil bli betegnet med Ω₁ og Ω₂. Under våre antakelser avhenger Ω_i bare av E_i. Vi antar også at en hvilken som helst mikrotilstand i system 1 som er i samsvar med E₁ kan eksistere sammen med hvilken som helst mikrotilstand i system 2 som er i samsvar med E₂. Dermed er antallet mikrotilstander for det kombinerte systemet

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}(E-E_{1}).\,}$

Vi vil utlede β fra den grunnleggende antagelsen om statistisk mekanikk:

Når det kombinerte systemet når likevekt, maksimeres tallet Ω.

(Med andre ord søker systemet naturlig nok det maksimale antallet mikrostater.) Derfor, ved likevekt,

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Men E₁ + E₂ = E tilsier

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Så

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

det vil si

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{ved likevekt.}}}$

Ovennevnte forhold motiverer en definisjon av β:

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Når to systemer er i likevekt, har de samme termodynamisk temperatur T . Dermed ville man intuitivt forvente at β (som definert via mikrotilstander) på en eller annen måte var relatert til T. Denne lenken er gitt av Boltzmanns grunnleggende antagelse skrevet som

${\displaystyle S=k_{\rm {B}}\ln \Omega ,\,}$

hvor k_B er Boltzmann-konstanten, S er den klassiske termodynamiske entropien, og Ω er antallet mikrotilstander. Så

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Å erstatte definisjonen av β fra den statistiske definisjonen ovenfor gir

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Sammenligning med termodynamisk formel

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

vi har

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

hvor ${\displaystyle \tau }$ kalles systemets grunntemperatur, og har energienheter.