Jedynka trygonometryczna – tożsamość trygonometryczna postaci[1]:

Jest ona prawdziwa dla każdej wartości kąta  a także ogólniej dla argumentów zespolonych.
a także ogólniej dla argumentów zespolonych.
Istnieją również dwie inne wariacje tego wzoru:


Dowód
Sposób 1:
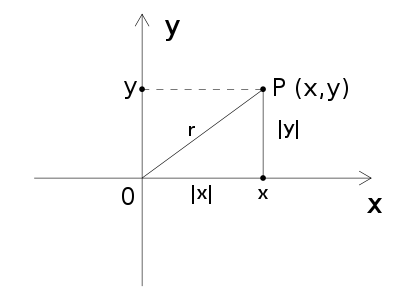
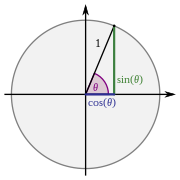
Niech 
Zauważmy, że:

więc trójkąt  jest trójkątem prostokątnym o przeciwprostokątnej
jest trójkątem prostokątnym o przeciwprostokątnej 
Zatem na mocy twierdzenia Pitagorasa:



Z definicji funkcji trygonometrycznych wyrażenie

jest równe

Zatem

q.e.d.
Zauważmy, że to rozumowanie można przeprowadzić również w drugą stronę, co oznacza, że wzór jedynkowy jest równoważny twierdzeniu Pitagorasa. Stąd jedna z jego nazw: postać trygonometryczna twierdzenia Pitagorasa.
Sposób 2:
Ze wzoru Eulera:

oraz

Zatem
![{\displaystyle {\begin{aligned}\sin ^{2}{x}+\cos ^{2}{x}&=\left({\frac {e^{ix}-e^{-ix}}{2i}}\right)^{2}+\left({\frac {e^{ix}+e^{-ix}}{2}}\right)^{2}\\[1ex]&={\frac {e^{2ix}-2+e^{-2ix}}{-4}}+{\frac {e^{2ix}+2+e^{-2ix}}{4}}\\&={\frac {2+2}{4}}=1,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/571ee4ba50ce26a8979e23daa6324a64c9727459)
q.e.d.
Stąd wynika, że jedynka trygonometryczna jest słuszna w dziedzinie liczb zespolonych.
Sposób 3:
Niech:

Zauważmy, że:

Także:

Skoro pochodna funkcji  jest równa 0, to funkcja
jest równa 0, to funkcja  musi być funkcją stałą.
musi być funkcją stałą.
Wiedząc, że  oraz że funkcja
oraz że funkcja  jest funkcją stałą, możemy dojść do wniosku, że
jest funkcją stałą, możemy dojść do wniosku, że

q.e.d.
Zobacz też
- funkcje trygonometryczne
- jedynka hiperboliczna
Przypisy
- ↑ Fritz Reinhardt, Heinrich Soeder: Atlas matematyki. Prószyński i S-ka, 2003, s. 183. ISBN 83-7469-189-1.
Trygonometria
| działy | - goniometria
- trygonometria sferyczna
|
|---|
funkcje
trygonometryczne | - sinus
- cosinus
- tangens
- cotangens
- secans
- cosecans
|
|---|
tożsamości
trygonometryczne | |
|---|
| inne twierdzenia | |
|---|
| zagadnienia | |
|---|
funkcje odwrotne –
cyklometryczne | - arcus sinus
- arcus cosinus
- arcus tangens
- arcus cotangens
- arcus secans
- arcus cosecans
|
|---|
| powiązane pojęcia | | geometryczne | |
|---|
| algebraiczne | |
|---|
| inne | |
|---|
|
|---|
powiązane działy
matematyki | |
|---|
| badacze | |
|---|
| pokrewne funkcje | |
|---|
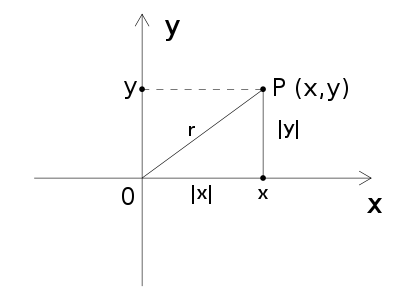

















![{\displaystyle {\begin{aligned}\sin ^{2}{x}+\cos ^{2}{x}&=\left({\frac {e^{ix}-e^{-ix}}{2i}}\right)^{2}+\left({\frac {e^{ix}+e^{-ix}}{2}}\right)^{2}\\[1ex]&={\frac {e^{2ix}-2+e^{-2ix}}{-4}}+{\frac {e^{2ix}+2+e^{-2ix}}{4}}\\&={\frac {2+2}{4}}=1,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/571ee4ba50ce26a8979e23daa6324a64c9727459)














