Kryterium całkowe

Kryterium całkowe (także kryterium całkowe Maclaurina-Cauchy’ego^[1]) – kryterium zbieżności szeregów o wyrazach dodatnich oparte na idei porównywania danego szeregu z całką. Wczesna forma tego kryterium została odkryta w Indiach przez Madhawę^[2] w XIV wieku i jego następców ze szkoły w Kerali. W Europie kryterium zostało później ponownie odkryte przez Maclaurina w 1742^[3] i Cauchy’ego^[4].

Niech ${\displaystyle f\colon [1,\infty )\to \mathbb {R} }$ będzie funkcją dodatnią i malejącą. Niech ponadto ${\displaystyle a_{n}=f(n)}$ dla każdego ${\displaystyle n.}$ Wówczas szereg

${\displaystyle \sum _{n=1}^{\infty }a_{n}}$

(A)

jest zbieżny wtedy i tylko wtedy, gdy zbieżna jest całka niewłaściwa^[5]

${\displaystyle \int \limits _{1}^{\infty }f(x)\,\mathrm {d} x.}$

(I)

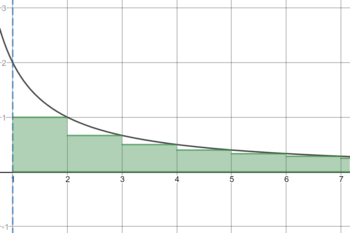
Całka (I) wyraża pole powierzchni pod krzywą ${\displaystyle y=f(x)}$ (na ilustracji obok zaznaczonej na czarno) na przedziale ${\displaystyle [1,\infty ).}$ Wyrazy szeregu (A) podają wielkość rzędnych wykresu w punktach ${\displaystyle x=1,2,\dots ,}$ a więc wyrażają pola prostokątów o podstawie ${\displaystyle 1}$ i wysokościach ${\displaystyle a_{n}}$ (na ilustracji obok zaznaczone na zielono). Suma szeregu (A) jest zatem sumą pól rzeczonych prostokątów. Biorąc to pod uwagę, kryterium całkowe można zinterpretować następująco: jeżeli pole pod wykresem ${\displaystyle y=f(x)}$ jest skończone, to tym bardziej skończona jest suma pól ${\displaystyle 1\cdot a_{n}}$ (równa sumie szeregu (A)). Dokonując przesunięcia każdego z prostokątów o ${\displaystyle 1}$ w prawo, wykres ${\displaystyle y=f(x)}$ na przedziale ${\displaystyle [2,\infty )}$ znajdzie się zawarty w figurze złożonej ze wspomnianych przesunięć. W szczególności, jeżeli pole pod wykresem ${\displaystyle y=f(x)}$ jest nieskończone, to nieskończone musi być także pole rozważanej figury, a więc i tym samym suma szeregu (A)^[6].

Ponieważ funkcja ${\displaystyle f}$ jest malejąca zachodzą nierówności

• ${\displaystyle f(x)\leqslant a_{k}}$ dla ${\displaystyle k\leqslant x\leqslant k+1,}$
• ${\displaystyle a_{k}\leqslant f(x)}$ dla ${\displaystyle k-1\leqslant x\leqslant k.}$

Oznacza to, że

${\displaystyle \int \limits _{k}^{k+1}f(x)\,\mathrm {d} x\leqslant a_{k}\leqslant \int \limits _{k-1}^{k}f(x)\,\mathrm {d} x\qquad (k\,=2,3\ldots ),}$

a stąd

${\displaystyle a_{2}+\ldots +a_{n}\leqslant \int \limits _{1}^{n}f(x)\,\mathrm {d} x\leqslant a_{1}+\ldots +a_{n-1}.}$

W przypadku gdy całka (I) jest zbieżna, ciąg całek częściowych

${\displaystyle {\bigg (}\int \limits _{1}^{k}f(x)\,\mathrm {d} x{\bigg )}_{k=1}^{\infty }}$

jest ograniczony, co pociąga ograniczoność ciągu sum częściowych

${\displaystyle {\bigg (}\sum _{j=1}^{k}a_{j}{\bigg )}_{k=1}^{\infty }}$

szeregu (A). Ciąg ten jest także niemalejący (z założenia, że wyrazy szeregu (A) są nieujemne), więc jako ograniczony i niemalejący ciąg liczb rzeczywistych jest on zbieżny, a tym samym szereg (A) jest zbieżny.

W przypadku, gdy szereg (A) jest zbieżny, wyżej zdefiniowany ciąg całek częściowych jest również ograniczony, a więc zbieżny (do całki (I)) jako ograniczony i niemalejący ciąg liczb rzeczywistych^[7].

• Szereg harmoniczny rzędu ${\displaystyle s{:}}$

${\displaystyle \sum _{n=m}^{\infty }{\frac {1}{n^{s}}}}$

jest zbieżny dla ${\displaystyle s>1.}$ Istotnie, funkcja ${\displaystyle f(x)=x^{-s}}$ jest dodatnia i malejąca na przedziale ${\displaystyle [1,\infty ),}$ więc stosuje się kryterium całkowe:

${\displaystyle \int \limits _{m}^{\infty }{\frac {\mathrm {d} x}{x^{s}}}=\int \limits _{m}^{\infty }{x^{-s}\mathrm {d} x}=\left[{\frac {x^{-s+1}}{-s+1}}\right]_{m}^{\infty }=\lim _{x\to \infty }~{\frac {x^{-s+1}}{-s+1}}-{\frac {m^{-s+1}}{-s+1}}=-{\frac {m^{-s+1}}{-s+1}},}$

gdy ${\displaystyle -s+1<0,}$ czyli gdy ${\displaystyle s>1}$^[7].

• Szereg

${\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n\cdot (\ln n)^{s}}}}$

jest zbieżny dla ${\displaystyle s>1}$ i rozbieżny w przeciwnym przypadku. Istotnie, oznaczając

${\displaystyle f(x)={\frac {1}{x\cdot (\ln x)^{s}}}\quad (x\geqslant 2),}$

mamy

${\displaystyle \int f(x)\,\mathrm {d} x={\frac {(\ln x)^{1-s}}{1-s}}+C,\quad s\neq 1,}$

${\displaystyle \int f(x)\,\mathrm {d} x=\ln(\ln x)+C,\quad s=1,}$

a stąd całka niewłaściwa ${\displaystyle \textstyle \int _{2}^{\infty }f(x)\,\mathrm {d} x}$ istnieje gdy ${\displaystyle s>1}$ oraz nie istnieje w przeciwnym przypadku^[8].

• Grigorij Michajłowicz Fichtenholz: Rachunek różniczkowy i całkowy. T. 2. Warszawa: Państwowe Wydawnictwo Naukowe, 1966.
• Franciszek Leja: Rachunek różniczkowy i całkowy. Wyd. 11. Warszawa: PWN, 1971.
• John Srdjan Petrovic: Advanced Calculus: Theory and Practice. Boca Raton, London, New York: CRC Press, 2014. ISBN 978-1466565630.