Pierwiastkowanie

Ten artykuł dotyczy odwrócenia potęgowania. Zobacz też: inne znaczenia słowa „pierwiastek”.

Ten artykuł od 2024-08 zawiera treści, przy których brakuje odnośników do źródeł. Należy dodać przypisy do treści niemających odnośników do źródeł. Dodanie listy źródeł bibliograficznych jest problematyczne, ponieważ nie wiadomo, które treści one uźródławiają. Sprawdź w źródłach: Encyklopedia PWN • Google Books • Google Scholar • Federacja Bibliotek Cyfrowych • BazHum • BazTech • RCIN • Internet Archive (texts / inlibrary) Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu. Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.

Pierwiastkowanie – operacja odwrotna względem potęgowania, zdefiniowana m. in. dla liczb rzeczywistych i zespolonych. Przy tym dla liczb rzeczywistych wprowadza się dwa pojęcia: pierwiastka arytmetycznego i pierwiastka algebraicznego.

Pierwiastki pojawiają się np. w definicji średniej geometrycznej, w pierwiastkowym kryterium Cauchy’ego na zbieżność szeregu liczbowego albo w definicji odległości Minkowskiego.

Pierwiastki zespolone z jedynki odgrywają istotną rolę w matematyce wyższej. Duża część teorii Galois skupia się na wskazaniu, które z liczb algebraicznych można przedstawić za pomocą pierwiastków, co prowadzi do twierdzenia Abela-Ruffiniego mówiącego, iż ogólny wielomian stopnia piątego bądź wyższego nie może być rozwiązany za pomocą tzw. pierwiastników, tzn. wyrażeń połączonych działaniami dodawania, odejmowania, mnożenia i dzielenia oraz pierwiastków.

Pierwiastki arytmetyczne definiuje się dla liczb rzeczywistych i w taki sposób, by przypisać liczbom rzeczywistym pierwiastki w sposób wzajemnie jednoznaczny, tj. każdej liczbie rzeczywistej odpowiada dokładnie jeden pierwiastek stopnia ${\displaystyle n}$-tego, przy czym nie istnieją pierwiastki arytmetyczne dla liczb ujemnych stopnia parzystego, np. pierwiastek drugiego stopnia z -1. Natomiast w dziedzinie liczb zespolonych pierwiastek ${\displaystyle n}$-tego stopnia z liczby -1 istnieje i ma ${\displaystyle n}$ wartości (por. dalej); w tym przypadku liczba -1 jest traktowana jako liczba zespolona o zerowej części urojonej. Także definiuje się tzw. pierwiastek algebraiczny w dziedzinie liczb rzeczywistych, który może mieć dwie wartości dla tej samej liczby.

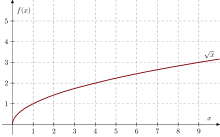
Pierwiastkiem arytmetycznym stopnia ${\displaystyle n=1,2,3,4\dots }$ z liczby rzeczywistej nieujemnej ${\displaystyle x\ (x\geq 0)}$ nazywamy taką liczbę rzeczywistą nieujemną ${\displaystyle y\ (y\geq 0)}$, która podniesiona do potęgi ${\displaystyle n}$ daje liczbę ${\displaystyle x}$, tj.

${\displaystyle y^{n}=x}$

i zapisuje się w postaci

${\displaystyle y={\sqrt[{n}]{x}}}$

W ten sposób każdej nieujemnej liczbie rzeczywistej przypisana zostaje jedna nieujemna liczba rzeczywista, będąca jej pierwiastkiem arytmetycznym.

Liczbę ${\displaystyle x}$ nazywamy liczbą podpierwiastkową.

Z definicji wynika, że pierwiastek stopnia ${\displaystyle n}$ z liczby ${\displaystyle x}$ jest pierwiastkiem równania ${\displaystyle y^{n}-x=0}$ zmiennej ${\displaystyle y}$ przy ustalonej wartości ${\displaystyle x}$.

Np. ${\displaystyle {\sqrt[{4}]{16}}=2}$ - pierwiastek arytmetyczny czwartego stopnia z ${\displaystyle 16}$, gdyż ${\displaystyle 2^{4}=16.}$

Uwaga: Jeżeli liczbę 16 będziemy traktować jako liczbę zespoloną (o zerowej części urojonej), to otrzymamy cztery pierwiastki ${\displaystyle {\sqrt[{4}]{16}}=2,-2,2i,-2i}$ (por. dalej - pierwiastki zespolone).

Dla liczb rzeczywistych ujemnych ${\displaystyle x<0}$ pierwiastek stopnia nieparzystego ${\displaystyle n}$ definiuje się wzorem

${\displaystyle y=-{\sqrt[{n}]{|x|}}}$

gdzie ${\displaystyle |x|}$ - wartość bezwzględna liczby ${\displaystyle x}$

Np.${\displaystyle {\sqrt[{3}]{-8}}=-\ {\sqrt[{3}]{8}}=-2,\quad }$ ${\displaystyle {\sqrt[{5}]{-2}}=-\ {\sqrt[{5}]{2}}=-1{,}148698354\dots }$

Dla nieparzystych ${\displaystyle n}$ każda liczba rzeczywista ma w ten sposób zdefiniowany pierwiastek rzeczywisty n-tego stopnia.

Nie istnieje zaś rzeczywisty pierwiastek stopnia parzystego z liczby ujemnej, np. ${\displaystyle {\sqrt[{4}]{-8}}.}$ Jednak w dziedzinie liczb zespolonych ${\displaystyle {\sqrt[{4}]{-8}}}$ ma aż cztery różne wartości (por. dalej - pierwiastki zespolone).

Pierwiastki zapisuje się zwykle za pomocą symbolu ${\displaystyle {\sqrt {^{^{\;}}}}}$ (zob. niżej), pierwiastkom stopnia drugiego, trzeciego, czwartego itd. z liczby ${\displaystyle x}$ odpowiadają kolejno symbole ${\displaystyle {\sqrt {x}},{\sqrt[{3}]{x}},{\sqrt[{4}]{x}}}$ itp. (zwyczajowo pomija się w zapisie stopień pierwiastka kwadratowego). Notacja ta nie budzi zastrzeżeń w stosunku do pierwiastków arytmetycznych, niemniej może prowadzić do sprzeczności w przypadku pierwiastków algebraicznych, dla których symbole te nie są jednoznaczne, gdyż istnieje wiele pierwiastków algebraicznych danej liczby (por. niżej).

Dla ${\displaystyle n=2}$ pierwiastek arytmetyczny nazywa się pierwiastkiem kwadratowym i oznacza ${\displaystyle {\sqrt {x}}}$,  pomijając cyfrę 2, zaś dla ${\displaystyle n=3}$ nazywa się pierwiastkiem sześciennym i oznacza ${\displaystyle {\sqrt[{3}]{x}}}$; pierwiastki wyższych stopni nazywa się wyłącznie liczbowo, np. „pierwiastek czwartego stopnia”.

Obliczanie pierwiastka ${\displaystyle n}$-tego stopnia jest operacją odwrotną do potęgowania, dlatego pierwiastkowanie można zapisywać jako potęgowanie o wykładniku ułamkowym, tj.

${\displaystyle {\sqrt[{n}]{x}}\equiv x^{1/n}.}$

Dowód:

Korzystając z twierdzenia o potędze ${\displaystyle (x^{a})^{b}=x^{a\cdot b}}$ potęgi mamy:

${\displaystyle (x^{1/n})^{n}=x^{{\frac {1}{n}}\cdot n}=x^{1}=x}$

Z drugiej strony, z definicji pierwiastka wynika, że ${\displaystyle n}$-ta potęga pierwiastka ${\displaystyle n}$-tego stopnia musi dać liczbę podpierwiastkową ${\displaystyle x,}$ tj.

${\displaystyle ({\sqrt[{n}]{x}})^{n}=x}$

Porównując obie równości dostajemy dowodzony wzór.

Jeżeli ${\displaystyle x,y}$ są nieujemnymi liczbami rzeczywistymi, zaś ${\displaystyle n,m}$ są dodatnimi liczbami całkowitymi, to:

• ${\displaystyle {\sqrt[{n}]{xy}}={\sqrt[{n}]{x}}{\sqrt[{n}]{y}}}$
• ${\displaystyle {\sqrt[{n}]{x/y}}={\frac {\sqrt[{n}]{x}}{\sqrt[{n}]{y}}}\quad {}}$ dla ${\displaystyle \ y\neq 0}$
• ${\displaystyle {\sqrt[{n}]{x^{m}}}=\left({\sqrt[{n}]{x}}\right)^{m}}$
• ${\displaystyle {\sqrt[{m}]{\sqrt[{n}]{x}}}={\sqrt[{m\cdot n}]{x}}}$

• gdy ${\displaystyle x<y}$ to ${\displaystyle {\sqrt[{n}]{x}}<{\sqrt[{n}]{y}}}$
• Pierwiastek kwadratowy z liczby naturalnej jest albo liczbą naturalną, albo niewymierną^[a]; np. dla liczby naturalnej 2:

${\displaystyle {\sqrt {2}}=1{,}414213562\dots }$

• Im większy stopień pierwiastka z liczby mniejszej od ${\displaystyle 1}$, tym większa jest jego wartość, która zmierza do 1 wraz ze wzrostem stopnia pierwiastka, np. ${\displaystyle {\sqrt[{2}]{0.4}}\approx 0{.}6<\quad {\sqrt[{5}]{0.4}}\approx 0{.}8<\quad {\sqrt[{100}]{0.4}}\approx 0{.}99}$
• Im większy stopień pierwiastka z liczby wiekszej od ${\displaystyle 1}$, tym mniejsza jest jego wartość, która zmierza do ${\displaystyle 1}$ wraz ze wzrostem stopnia pierwiastka, np. ${\displaystyle {\sqrt {2}}\approx 1{,}4>\quad {\sqrt[{3}]{2}}\approx 1{,}3>\quad {\sqrt[{100}]{2}}\approx 1{,}007}$

• Pierwiastki stopni całkowitych z liczb niewymiernych są niewymierne, bo liczba wymierna podniesiona do potęgi o dowolnym wykładniku całkowitym daje liczbę wymierną.

Pierwiastkiem algebraicznym stopnia ${\displaystyle n}$ (gdzie ${\displaystyle n=1,2,\dots }$) z liczby rzeczywistej ${\displaystyle x}$ nazywamy taką liczbę rzeczywistą ${\displaystyle y}$ (dodatnią lub ujemną lub równą zero), która podniesiona do potęgi ${\displaystyle n}$ daje liczbę ${\displaystyle x}$^[1], tj.

${\displaystyle y^{n}=x}$

Pierwiastek algebraiczny z liczb rzeczywistych ujemnych stopnia parzystego nie istnieje, podobnie jak pierwiastek arytmetyczny stopnia parzystego, np. pierwiastek kwadratowy z ${\displaystyle -8}$. Ale istnieje pierwiastek algebraiczny dla dowolnych liczb rzeczywistych stopnia nieparzystego i ma zawsze jedną wartość, np. pierwiastek 3-go stopnia z ${\displaystyle -8}$ wynosi ${\displaystyle -2}$. Zaś dla liczb rzeczywistych dodatnich istnieją zawsze dwa pierwiastki algebraiczne stopnia parzystego. Np. dla liczby ${\displaystyle 4}$ istnieją dwie takie liczby: ${\displaystyle 2}$ oraz ${\displaystyle -2}$, gdyż ${\displaystyle 2^{2}=4}$ oraz ${\displaystyle (-2)^{2}=4}$ - obie te liczby nazywamy pierwiastkami kwadratowymi algebraicznymi z liczby ${\displaystyle 4}$.

Operacja znajdowania pierwiastka algebraicznego w dziedzinie liczb rzeczywistych przypisuje więc danej liczbie jedną wartość lub dwie wartości, inaczej niż dla pierwiastka arytmetycznego, który przyjmuje zawsze jedną wartość (oraz - tak jak w przypadku pierwiastka arytmetycznego - wyklucza przypisywanie pierwiastków stopnia parzystego liczbom ujemnym).

Df. Pierwiastkiem zespolonym stopnia ${\displaystyle n=1,2,3,4\dots }$ z liczby zespolonej ${\displaystyle z}$ nazywa się dowolną liczbę ${\displaystyle w}$ spełniającą równość

${\displaystyle w^{n}=z}$

Każda niezerowa liczba zespolona ${\displaystyle z}$ (w tym liczba rzeczywista, tj. zespolona o zerowej części urojonej) ma ${\displaystyle n}$ różnych zespolonych pierwiastków ${\displaystyle n}$-tego stopnia.

Tw. Aby wyznaczyć pierwiastki zespolone liczby zespolonej ${\displaystyle z=a+ib}$, przedstawia się ją w postaci trygonometrycznej:

${\displaystyle z=|z|\left(\cos \phi +i\sin \phi \right)}$

gdzie:

${\displaystyle |z|={\sqrt {a^{2}+b^{2}}}}$ - moduł

${\displaystyle \phi =\arctan(b/a)\in (-\pi ,\pi >}$ - argument główny

Wtedy pierwiastki ${\displaystyle n}$-go stopnia określa wzór de Moivre’a:

${\displaystyle w_{(k)}={\sqrt[{n}]{|z|}}\left(\cos {\tfrac {\phi +2k\pi }{n}}+i\sin {\tfrac {\phi +2k\pi }{n}}\right),}$

gdzie ${\displaystyle k=0,1,2,\dots ,n-1}$ oznacza numer pierwiastka (symbol ${\displaystyle {\sqrt[{n}]{\;}}}$ oznacza tu pierwiastek arytmetyczny).

Interpretacja geometryczna: W interpretacji geometrycznej punkty przedstawiające pierwiastki stopnia ${\displaystyle n}$ liczby zespolonej tworzą wierzchołki ${\displaystyle n}$-kąta foremnego mającego środek w początku układu współrzędnych, wpisanego w okrąg o promieniu ${\displaystyle {\sqrt[{n}]{|z|}},}$ przy czym wektor wodzący wierzchołka o indeksie 0 jest pod katem ${\displaystyle \phi /n}$ do osi rzeczywistej układu współrzędnych. Ilustrują to przykłady.

Przykłady

Przykład 1: Pierwiastek kwadratowy z ${\displaystyle z=i}$

Niech będzie dana liczba czysto urojona ${\displaystyle z=i.}$ Liczba ta ma zerową część rzeczywistą, tj. ${\displaystyle z=0+1\cdot i}$ . Mamy więc moduł ${\displaystyle |z|=1}$, argument główny ${\displaystyle \phi =\pi /2}$, stąd postać trygonometryczna ${\displaystyle z=i=\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}}.}$

Z wzoru Moivre'a mamy pierwiastki 2-go stopnia z ${\displaystyle z=i}$

${\displaystyle w_{0}=\cos {\tfrac {\pi }{4}}+i\sin {\tfrac {\pi }{4}}={\tfrac {1}{\sqrt {2}}}+i{\tfrac {1}{\sqrt {2}}}}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{2}}+i\sin {\tfrac {3\pi }{2}}=-{\tfrac {1}{\sqrt {2}}}-i{\tfrac {1}{\sqrt {2}}}}$

Pierwiastki te są leżą po przeciwnych stronach początku układu współrzędnych.

Przykład 2: Pierwiastki 2-go stopnia z -1

Niech będzie dana liczba ${\displaystyle z=-1.}$ W dziedzinie liczb rzeczywistych nie istnieje pierwiastek algebraiczny z liczby ujemnej stopnia parzystego. Jednak w dziedzinie liczb zespolonych liczba -1 jest liczbą o zerowej części urojonej i ma de facto postać ${\displaystyle z=-1+0\cdot i}$ . Mamy więc moduł ${\displaystyle |z|=1}$, argument główny ${\displaystyle \phi =\pi }$, stąd postać trygonometryczna ${\displaystyle z=-1=\cos \pi +i\sin \pi .}$

Z wzoru Moivre'a mamy pierwiastki 2-go stopnia z ${\displaystyle z=-1}$

${\displaystyle w_{0}=\cos {\tfrac {\pi }{2}}+i\sin {\tfrac {\pi }{2}}=i}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{2}}+i\sin {\tfrac {3\pi }{2}}=-i}$

W dziedzinie zespolonej istnieją wiec dwa pierwiastki kwadratowe z ${\displaystyle z=-1:+i,-i.}$ (Każda liczba zespolona jest punktem na płaszczyźnie, w tym -1, sytuacja jest więc inna, niż w przypadku obliczania pierwiastków w dziedzinie rzeczywistej, gdzie liczby są punktami na prostej).

Przykład 3: Pierwiastki 3-go stopnia z -1

Aby obliczyć pierwiastki 3-go stopnia korzystamy z postaci trygonometrycznej ${\displaystyle z=-1=\cos \pi +i\sin \pi }$ oraz wzoru Moivre'a:

${\displaystyle w_{0}=\cos {\tfrac {\pi }{3}}+i\sin {\tfrac {\pi }{3}}={\tfrac {1}{2}}+i{\tfrac {\sqrt {3}}{2}}}$

${\displaystyle w_{1}=\cos {\tfrac {3\pi }{3}}+i\sin {\tfrac {3\pi }{3}}=-1}$

${\displaystyle w_{2}=\cos {\tfrac {4\pi }{3}}+i\sin {\tfrac {4\pi }{3}}={\tfrac {1}{2}}-i{\tfrac {\sqrt {3}}{2}}}$

Przykłady powyższe ilustrują ogólna prawidłowość, iż każda liczba zespolona ${\displaystyle z}$ ma ${\displaystyle n}$ pierwiastków ${\displaystyle n}$-tego stopnia - w tym liczby zespolone czysto rzeczywiste, które nie mają pierwiastków algebraicznych w dziedzinie liczb rzeczywistych.

W dziedzinie pierwiastków zespolonych obowiązują te same twierdzenia, co w dziedzinie liczb rzeczywistych, ale posługiwanie się nimi wymaga uwagi ze względu na wielowartościowość pierwiastków zespolonych. Np. zakładając słuszność twierdzenia ${\displaystyle {\sqrt[{n}]{z_{1}\cdot z_{2}}}\ ={\sqrt[{n}]{z}}_{1}{\sqrt[{n}]{z}}_{2}}$ otrzymamy

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}={\sqrt {-1\cdot -1}}}$

Ale

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}=i\cdot i=i^{2}=-1}$

zaś

${\displaystyle {\sqrt {-1\cdot -1}}={\sqrt {1}}=1}$

- czyli sprzeczność. Sprzeczność wynika stąd, że w obliczeniach nie uwzględniono faktu, iż pierwiastki kwadratowe z liczb ${\displaystyle {\sqrt {-1}}}$ oraz ${\displaystyle {\sqrt {1}}}$ w dziedzinie liczb zespolonych mają po dwie wartości:

${\displaystyle {\sqrt {-1}}={\begin{cases}+i\\-i\end{cases}}\quad }$ oraz ${\displaystyle \quad {\sqrt {1}}={\begin{cases}+1\\-1\end{cases}}}$

Wtedy mamy:

${\displaystyle {\sqrt {-1}}\cdot {\sqrt {-1}}={\begin{cases}i\cdot i=-1\\{\text{lub}}\\i\cdot (-i)=1\end{cases}}\quad }$

czyli dostajemy dwa wyniki, identyczne jak dla pierwiastka z 1.

Początki symbolu pierwiastka √ są dość niejasne. Niektóre źródła^{[potrzebny przypis]} podają, że symbol został wprowadzony przez Arabów, a po raz pierwszy został on użyty przez Abū al-Hasana ibn Alīego al-Qalasādīego (1421–1486) i został wyprowadzony z arabskiej litery ج, pierwszej litery słowa جذر (dżazr) oznaczającego „korzeń”. Wielu, w tym Leonhard Euler^[2] sądziło, że pochodzi on od litery r, pierwszej litery łacińskiego słowa radix (również oznaczającego „korzeń”), które oznacza to samo działanie matematyczne.

Nieużywany w języku polskim termin surd, traktowany niekiedy jako nazwa symbolu √^[3], pochodzi z czasów al-Khwārizmīego (ok. 825), który liczby wymierne i niewymierne nazywał odpowiednio „słyszalnymi” i „niesłyszalnymi”. W związku z tym arabskie assam („głuchy, głupi”) oznaczające liczbę niewymierną było później tłumaczone na łacinę jako surdus („głuchoniemy”). Gerard z Cremony (ok. 1150), Fibonacci (1202), a potem Robert Recorde (1551) używali tego terminu w odniesieniu do nierozwiązanych pierwiastków niewymiernych^[4].

Symbolu √ użyto po raz pierwszy w druku bez vinculum (poziomej kreski nad liczbami wewnątrz symbolu pierwiastka) w 1525 roku w Die Coss autorstwa niemieckiego matematyka Christoffa Rudolffa. Vinculum wprowadził Kartezjusz w Geometrii (1637) do zaznaczania, jakie wyrażenie algebraiczne podlega pierwiastkowaniu^[3].

Stosowana przez Kartezjusza notacja dla pierwiastków stopnia wyższego niż dwa nie przyjęła się (np. ${\displaystyle {\sqrt[{3}]{x}}}$ Kartezjusz zapisywał jako ${\displaystyle {\sqrt {C.x}}}$^[b])^[3]. Współczesną notację stopnia pierwiastka zaproponował Albert Girard w pracy z 1629 roku; utrwaliła się ona w pierwszej połowie XVIII w.^[5]

Niżej przedstawiono kody znaków symboli pierwiastka. W notacji angielskiej znak pierwiastka występuje bez wiążącej kreski górnej^[6].

W LaTeX-u:

• pierwiastek ${\displaystyle {\sqrt {x}}}$ zapisywany jest jako \sqrt x;
• pierwiastek ${\displaystyle {\sqrt[{k}]{x}}}$ zapisywany jest jako \sqrt[k] x.

Zobacz hasło pierwiastkowanie w Wikisłowniku

• pierwiastek kwadratowy
• pierwiastek sześcienny
• pierwiastki zespolone z jedynki
• wzór de Moivre'a
• algorytm Newtona numerycznego obliczania pierwiastka n-tego stopnia (dla liczby rzeczywistej)

Inne:

• Pomoc Wikipedii: Pierwiastki we wzorach matematycznych - nt. edycji wzorów za pomocą kodu

• I. N. Bronsztejn, K. A. Siemiendiajew, Poradnik encyklopedyczny Matematyka, PWN, Warszawa 2019, str. 578-579.
• T. Trajdos, Matematyka dla inżynierów, PWN, Warszawa 1974, str. 412-416.