Wzory redukcyjne – wzory pozwalające sprowadzić obliczanie wartości funkcji trygonometrycznych dowolnego kąta skierowanego do obliczenia wartości funkcji dla kąta ostrego, a dalej dla kąta o mierze z zakresu od 90° do 180°
W poniższych wzorach używana jest miara łukowa kąta. Korzystając z miary stopniowej należy w poniższych wzorach podstawić 180° w miejsce π.
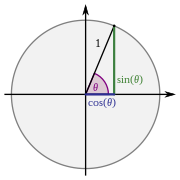
Sinus i cosinus
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Tangens i cotangens
 |  |
 |  |
 |  |
 |  |
 |  |
Podawanie wzorów typu  nie jest potrzebne, bo okresem funkcji tangens i cotangens jest π.
nie jest potrzebne, bo okresem funkcji tangens i cotangens jest π.
Wzory redukcyjne można wywieść z symetrii wykresów odpowiednich funkcji trygonometrycznych. Mianowicie, wykres funkcji sinus jest środkowo symetryczny względem dowolnego punktu osi OX o współrzędnej postaci kπ i osiowo symetryczny względem dowolnej prostej o równaniu x = π/2 + kπ. Dla cosinusa odpowiednie symetrie wypadają dla x =π/2 + kπ oraz x = kπ. Dla tangensa i cotangensa mamy jedynie symetrie środkowe odpowiednio względem punktów x=kπ oraz x=π/2 + kπ.
Interpretacja na wykresie
Wykresy pozwalają też na wyobrażenie sobie (i szybkie odtworzenie w pamięci lub na kartce) wzorów redukcyjnych.
1. W tym celu trzeba tylko zapamiętać jak wyglądają wykresy funkcji trygonometrycznych. Następnie przekształcamy wykres tej funkcji, którą mamy obliczyć:
- jeśli w argumencie jest
 gdzie
gdzie  jest równe np.
jest równe np. 

 lub
lub  to przesuwamy wykres odpowiedniej funkcji o
to przesuwamy wykres odpowiedniej funkcji o  w lewo.
w lewo. - jeśli w argumencie jest
 to przesuwamy wykres o
to przesuwamy wykres o  w prawo.
w prawo. - jeśli w argumencie jest
 to przesuwamy wykres o
to przesuwamy wykres o  w lewo i odbijamy wykres symetrycznie względem osi OY.
w lewo i odbijamy wykres symetrycznie względem osi OY.
2. Jeśli przed funkcją stoi minus, odbijamy wykres względem osi OX.
3. Na koniec spoglądamy na powstały wykres w miejscu, w którym przecina oś OY:
- Jeśli przecina ją w punkcie
 to wynikiem jest
to wynikiem jest 
- Jeśli przecina ją w punkcie
 to wynikiem jest
to wynikiem jest 
- Jeśli przecina ją w środku układu współrzędnych i rośnie, to wynikiem jest
 (gdy przekształcaliśmy sinus lub cosinus) lub
(gdy przekształcaliśmy sinus lub cosinus) lub  (gdy przekształcaliśmy tangens lub cotangens)
(gdy przekształcaliśmy tangens lub cotangens) - Jeśli przecina ją w środku układu współrzędnych i maleje, to wynikiem jest
 (gdy przekształcaliśmy sinus lub cosinus) lub
(gdy przekształcaliśmy sinus lub cosinus) lub  (gdy przekształcaliśmy tangens lub cotangens)
(gdy przekształcaliśmy tangens lub cotangens) - Jeśli w ogóle nie przecina osi OY, a w przedziale od 0 do
 rośnie, to wynikiem jest
rośnie, to wynikiem jest 
- Jeśli w ogóle nie przecina osi OY, a w przedziale od 0 do
 maleje, to wynikiem jest
maleje, to wynikiem jest 
Przykłady zastosowania
Dla odmiany użyta zostanie miara stopniowa. Należy pamiętać, że funkcje trygonometryczne są okresowe – jeżeli miara kąta przekracza 360° można wyodrębnić z niej wielokrotność 360° i przeprowadzać obliczenia dla pozostałej części.





W obu ostatnich przykładach pominięto okres funkcji.
Linki zewnętrzne
Trygonometria
| działy | - goniometria
- trygonometria sferyczna
|
|---|
funkcje
trygonometryczne | - sinus
- cosinus
- tangens
- cotangens
- secans
- cosecans
|
|---|
tożsamości
trygonometryczne | |
|---|
| inne twierdzenia | |
|---|
| zagadnienia | |
|---|
funkcje odwrotne –
cyklometryczne | - arcus sinus
- arcus cosinus
- arcus tangens
- arcus cotangens
- arcus secans
- arcus cosecans
|
|---|
| powiązane pojęcia | | geometryczne | |
|---|
| algebraiczne | |
|---|
| inne | |
|---|
|
|---|
powiązane działy
matematyki | |
|---|
| badacze | |
|---|
| pokrewne funkcje | |
|---|
 Paweł Lubowiecki, Funkcje trygonometryczne cz. II Wzory redukcyjne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].
Paweł Lubowiecki, Funkcje trygonometryczne cz. II Wzory redukcyjne, Wojskowa Akademia Techniczna im. Jarosława Dąbrowskiego, kanał „Uczelnia WAT” na YouTube, 30 stycznia 2024 [dostęp 2024-09-07].































































