Pêndulo cônico

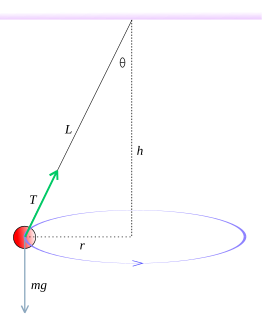
O pêndulo cônico é constituído por uma esfera presa a um suporte por meio de um fio. Ao contrário do pêndulo simples, que descreve um movimento oscilatório, o pêndulo cônico descreve um movimento circular. O fio que prende a esfera ao suporte descreve um cone, sendo este o motivo de seu nome.

O Pêndulo Cônico foi estudado inicialmente por Robert Hooke em 1660. Em 1679 Hooke enviou uma carta a Newton para explicar o Movimento Celestes e propor que a força centrípeta com que o Sol puxava os planetas variava com o inverso do quadrado da distância ao Sol, ele utilizou o Pêndulo Cônico para fazer está analogia.^[1]

Em 1666 Isaac Newton utilizou o Pêndulo Cônico para calcular a aceleração gravitacional que ele utilizaria no calculo da Força no Movimento circular.^[2]

O Pêndulo Cônico é utilizado no Governador centrífugo, um dispositivo que controla a velocidade do motor através da regulação da admissão de combustível, presente normalmente nos motores a vapor.

Nos dispondo das Leis de Newton podemos analisar o movimento circular descrito pela esfera e assim calcular o valor da aceleração gravitacional.

Considere a esfera um corpo puntiforme e o fio de massa nula e inextensível.

Equação da Segunda Lei de Newton:

${\displaystyle {\vec {Fr}}=m.{\vec {a}}}$

Igualando as forças que atuam sobre a esfera. As forças presentes neste sistema são o Peso que puxa a esfera em direção ao centro da terra (para baixo) e a Tração que puxa a esfera em direção ao ponto que a fixa no plano:

${\displaystyle {\vec {P}}+{\vec {T}}=m.{\vec {a}}}$

Decompondo essas forças entre os eixos cartesianos X e Y, temos:

${\displaystyle -P+T.cos(\theta )=0}$ em (Y) [equação 1]

${\displaystyle T.sen(\theta )=m.w^{2}.r}$ em (X) [equação 2]

Através da resolução deste sistema podemos chegar a equação que descreverá a aceleração gravitacional.

Isolando a Tração na equação em (Y):

${\displaystyle T.cos(\theta )=m.g}$

${\displaystyle T={\frac {m.g}{cos(\theta )}}}$ [equação 3]

Substituindo a [equação 3] na [equação 2] e resolvendo:

${\displaystyle {\frac {m.g}{cos(\theta )}}.sen(\theta )=m.w^{2}.r}$ ${\displaystyle \Longrightarrow }$ ${\displaystyle g={\frac {w^{2}.r.cos(\theta )}{sen(\theta )}}}$

Substituindo ${\displaystyle r=L.sen(\theta )}$:

${\displaystyle g={\frac {w^{2}.L.sen(\theta ).cos(\theta )}{sen(\theta )}}}$ ${\displaystyle \Longrightarrow }$ ${\displaystyle g=w^{2}.L.cos(\theta )}$

Substituindo ${\displaystyle w^{2}=({\frac {2\pi }{\tau }})^{2}}$:

${\displaystyle g=({\frac {2\pi }{\tau }})^{2}.L.cos(\theta )}$

Substituindo ${\displaystyle L.cos(\theta )=h}$:

${\displaystyle g={\frac {4\pi ^{2}}{\tau ^{2}}}.h}$

Através desta forma, sabendo o período de rotação da esfera e a altura dela em relação ao plano ao qual ela está fixada podemos calcular a Aceleração da gravidade.