Fenomenul Runge

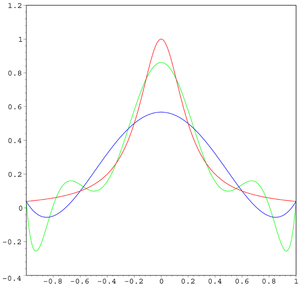
În analiză numerică, fenomenul Runge este o problemă de oscilație la marginile de un interval care se produce la utilizarea unui polinom de interpolare de un grad ridicat. Acest fenomen a fost descoperit de către Carl David Tolmé Runge când explora comportamentul erorilor atunci când se utilizează polinoame de interpolare pentru aproximarea anumitor funcții.^[1] În examinarea acestui aspect, matematicianul David Carle Runge Tolmé a descoperit un rezultat contrar intuiției: există configurații în care diferența între funcția de interpolare și cea interpolată este mare și tinde la infinit odată cu n.

Teorema de aproximare a lui Weierstrass prevede că fiecare funcție continuă f (x) definită pe un interval [a, b ] poate fi aproximată ca limita unui șir uniform convergent de polinoame de interpolare:

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}|f(x)-P_{n}(x)|\right)=0.}$

Interpolarea cu puncte echidistante este o abordare naturală și binecunoscută pentru a construi polinoame aproximare. Fenomenul Runge demonstrează, totuși, că această interpolare poate fi divergentă.

Considerăm următoarea funcție:

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}}$

Având în vedere ${\displaystyle (n+1)}$ puncte uniform distribuite în segmentul ${\displaystyle [-1,1]}$:

${\displaystyle \scriptstyle x_{0}=-1,\;x_{1}=x_{0}+h,\;\cdots ,\;x_{k+1}=x_{k}+h=x_{0}+(k+1)h,\;\cdots ,\;x_{n}=1\ {\text{cu}}\ h=\textstyle {\frac {2}{n}}}$

În cele din urmă, considerăm polinomul de interpolare ${\displaystyle f}$ în punctele ${\displaystyle (x_{i})}$, care este polinomul unic ${\displaystyle P}$de grad mai mic sau egal cu n astfel încât ${\displaystyle P(x_{i})=f(x_{i})}$ pentru orice i. Se notează cu ${\displaystyle P_{n}}$.

Runge a arătat că eroarea de interpolare între ${\displaystyle P_{n}}$ și ${\displaystyle f}$ tinde la infinit ca n crește. Formal:

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=\infty }$

De fapt, atunci când creșterea numărului de puncte, vom vedea că polinomul începe să oscileze puternic între punctele de ${\displaystyle x_{i}}$ cu amplitudinea în creștere.

Aplicând în mod repetat teorema lui Rolle, putem arăta că în cazul interpolării celor ${\displaystyle (n+1)}$ puncte distribuite în mod egal, există un punct în intervalul ${\displaystyle \xi \in [-1;1]}$ încât eroarea dintre funcția generatoare și polinomul de interpolare de grad n este dată de

${\displaystyle f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=1}^{n+1}(x-x_{i})}$

pentru ${\displaystyle \xi }$ între (−1, 1). Astfel,

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq \max _{-1\leq x\leq 1}{\frac {|f^{(n+1)}(x)|}{(n+1)!}}\max _{-1\leq x\leq 1}\prod _{i=0}^{n}|x-x_{i}|.}$

Rezultă că eroarea de aproximare crește la infinit odată cu n.

Într-un context mai larg, polinomul de interpolare cu noduri echidistante nu este o metodă stabilă. Într-adevăr, notând (l_i) , polinoamele Lagrange de bază corespunzătoare elementelor (x_i):

${\displaystyle l_{j}(x):=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{m}}{x_{j}-x_{m}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}.}$

avem:

${\displaystyle P_{n}(x)=\sum _{i=0}^{n}f(x_{i})l_{i}(x),}$

care ne conduce la următoarea estimare:

${\displaystyle \left|P_{n}(x)\right|\leqslant \left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)\|f\|_{\infty }\leqslant \sup _{x\in [a,b]}\left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)\|f\|_{\infty }.}$

Constanta ${\displaystyle \Lambda _{n}=\sup _{x\in [a,b]}\left(\sum _{i=0}^{n}\left|l_{i}(x)\right|\right)}$ este numită constanta Lebesgue asociată punctelor (xi)'. În caz de puncte echidistante, această constantă poate fi estimată prin:

${\displaystyle \Lambda _{n}\sim {\frac {2^{n+1}}{e\,n\ln(n)}},}$

unde e este numărul lui Euler în valoare de 2.7183 ... . Vedem că, în acest caz, constanta Lebesgue tinde rapid la valori mari, mai repede decât poate converge la funcția polinomială de interpolaref^[2].

Fenomenul Runge demonstrează că interpolarea polinomială nu este cea mai bună metodă de interpolare a funcțiilor.

Putem minimiza oscilațiile de polinoame de interpolare folosind polinomul Cebîșev de interpolare în loc de puncte distribuite în mod egal pentru a interpola. În acest caz, putem arăta că eroarea de interpolare ${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|}$ descrește.

O metodă este utilizarea de noduri care sunt distribuite mult mai dens spre marginile intervalului. ^[3]

O altă metodă este metoda celor mai mici pătrate. ^[4]

O altă metodă foarte des întâlnită este aproximarea cu funcții spline (acestea sunt polinoame pe porțiuni; în acest caz, pentru a îmbunătăți aproximarea, vom crește numărul de bucăți și nu gradul de polinoame).

• Jean Dieudonné, Calcul infinitésimal Format:Détail des éditions, chap. IX, appendice (pp. 319-320)

• http://an.lmn.pub.ro/lab/AN_Lab_4_v2.pdf
• www.ingineriebraila.ugal.ro/IngMec/An%20II-22-PA.doc