Byte av integrationsordning

Byte av integrationsordning är en central operation vid beräkningen av multipla integraler. En fråga som ofta dyker upp är om

${\displaystyle \iint _{X\times Y}f(x,y)\,dxdy=\int _{Y}\left(\int _{X}f(x,y)\,dx\right)dy=\int _{X}\left(\int _{Y}f(x,y)\,dy\right)dx.}$

${\displaystyle X}$ och ${\displaystyle Y}$ är rummen som integralerna är definierade över, till exempel de reella talen.

Följande två kriterier är var för sig tillräckliga för att ovanstående likheter skall gälla:

1. ${\displaystyle f(x,y)\geq 0\,}$ för alla ${\displaystyle x\in X\,}$ och ${\displaystyle y\in Y\,}$.
2. ${\displaystyle \iint _{X\times Y}|f(x,y)|\,dxdy<\infty }$

Ofta sker beräkningen i praktiken genom att kriterium 1 används på ${\displaystyle |f(x,y)|\,}$ för att visa att kriterium 2 kan användas. Se exempel nedan.

Det första kriteriet brukar kallas Tonellis sats och det andra för Fubinis sats. De gäller allmänt för väldigt generella integraler, definierade med hjälp av mått.

Betrakta funktionen

${\displaystyle f(x,y)=\sin(x)\sin(y)e^{-x^{2}-y^{2}}}$ .

Denna funktion växlar tecken många gånger, så kriterium 2 måste användas för att kunna beräkna integralen av ${\displaystyle f}$.

Först måste det alltså verifieras att kriterium 2 går att använda. Detta görs genom att betrakta integralen av ${\displaystyle |f|}$. Detta är en positiv funktion och det går alltså att byta integrationsordning enligt kriterium 1:

${\displaystyle \iint _{\mathbf {R} ^{2}}|f(x,y)|\,dxdy=\iint _{\mathbf {R} ^{2}}\left|\sin(x)\sin(y)e^{-x^{2}-y^{2}}\right|\,dxdy\leq \iint _{\mathbf {R} ^{2}}\left|e^{-x^{2}-y^{2}}\right|\,dxdy}$

${\displaystyle =\int _{-\infty }^{\infty }\left(\int _{-\infty }^{\infty }e^{-x^{2}-y^{2}}\,dx\right)dy=\int _{-\infty }^{\infty }e^{-y^{2}}{\sqrt {\pi }}dy=\pi <\infty }$.

Alltså är kriterium 2 uppfyllt och den ursprungliga integralen kan beräknas:

${\displaystyle \iint _{\mathbf {R} ^{2}}\sin(x)\sin(y)e^{-x^{2}-y^{2}}\,dxdy=\int _{-\infty }^{\infty }\sin(y)e^{-y^{2}}\left(\int _{-\infty }^{\infty }\sin(x)e^{-x^{2}}\,dx\right)dy=}$

${\displaystyle \int _{-\infty }^{\infty }\sin(y)e^{-y^{2}}\cdot 0\,dy=0}$.

Att det inte alltid går att byta ordning på integraler illustreras av följande exempel:

${\displaystyle \int _{1}^{\infty }{\frac {x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}}\ dy=\left[{\frac {y}{x^{2}+y^{2}}}\right]_{1}^{\infty }=-{\frac {1}{1+x^{2}}}.}$

och därför:

${\displaystyle \int _{1}^{\infty }\left(\int _{1}^{\infty }{\frac {x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}}\ dy\right)\ dx=-{\frac {\pi }{4}}\ .}$

${\displaystyle \int _{1}^{\infty }\left(\int _{1}^{\infty }{\frac {x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}}}\ dx\right)\ dy={\frac {\pi }{4}}\ .}$

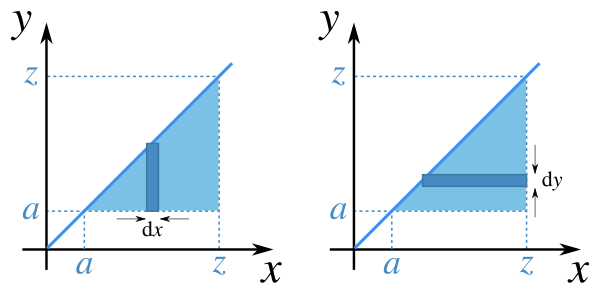
Integering över det triangelformade området kan se på två olika sätt: först i x-led och sen i y-led, och tvärtom.

• G. B. Folland, Real Analysis: Modern Techniques and Their Applications, John Wiley and Sons 1999 ISBN 0-471-31716-0

Den här artikeln ingår i boken:  Måtteori