Distribució de Yule-Simon

Distribució de Yule – Simon

Funció de densitat de probabilitat 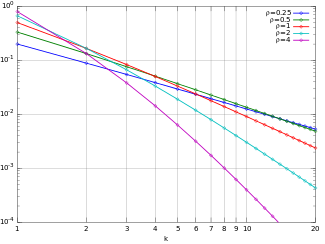Funció densitat de la distribució de Yule–Simon en escales logarítmiques. (Nota: La funció solament és definida per a valors enters de k. Les línies no indiquen continuïtat)
Funció de distribució de probabilitat 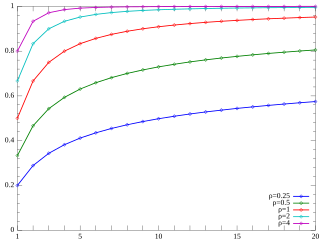Funció densitat acumulada. (Nota: La funció solament és definida per a valors enters de k. Les línies no indiquen continuïtat)
Tipus	distribució univariant i distribució de probabilitat discreta
Epònim	George Udny Yule i Herbert Simon
Paràmetres	${\displaystyle \rho >0\,}$ (real)
Suport	${\displaystyle k\in \{1,2,\dotsc \}}$
fdp	${\displaystyle \rho \operatorname {B} (k,\rho +1)}$
FD	${\displaystyle 1-k\operatorname {B} (k,\rho +1)}$
Esperança matemàtica	${\displaystyle {\frac {\rho }{\rho -1}}}$ for ${\displaystyle \rho >1}$
Moda	${\displaystyle 1}$
Variància	${\displaystyle {\frac {\rho ^{2}}{(\rho -1)^{2}(\rho -2)}}}$ per a ${\displaystyle \rho >2}$
Coeficient de simetria	${\displaystyle {\frac {(\rho +1)^{2}{\sqrt {\rho -2}}}{(\rho -3)\rho }}\,}$ per a ${\displaystyle \rho >3}$
Curtosi	${\displaystyle \rho +3+{\frac {11\rho ^{3}-49\rho -22}{(\rho -4)(\rho -3)\rho }}}$ per a ${\displaystyle \rho >4}$
FC	${\displaystyle {\frac {\rho }{\rho +1}}{}_{2}F_{1}(1,1;\rho +2;e^{i\,t})e^{i\,t}}$

En Probabilitat i Estadística, la distribució de Yule-Simon és una distribució de probabilitat discreta anomenada així en honor d'Udny Yule i Herbert A. Simon. Simon originalment la va anomenar distribució de Yule.^[1]

La funció densitat de probabilitat (fdp) de la distribució de Yule-Simon (ρ) és:

${\displaystyle f(k;\rho )=\rho \operatorname {B} (k,\rho +1)}$,

per un enter k ≥ 1 i ρ > 0 real, on B és la funció beta. De manera equivalent la fdp es pot escriure en termes de factorials com:

${\displaystyle f(k;\rho )={\frac {\rho \Gamma (\rho +1)}{(k+\rho )^{\underline {\rho +1}}}}}$

on ${\displaystyle \Gamma }$ es la funció gamma. Així si ρ és un enter:

${\displaystyle f(k;\rho )={\frac {\rho \,\rho !\,(k-1)!}{(k+\rho )!}}}$.

El paràmetre ρ es pot estimar utilitzant un algoritme de punt fix.^[2] La funció densitat de probabilitat ${\displaystyle f(k;\rho )}$ té la propietat que per a k prou gran tenim

${\displaystyle f(k;\rho )\approx {\frac {\rho \Gamma (\rho +1)}{k^{\rho +1}}}\propto {\frac {1}{k^{\rho +1}}}}$.

Això vol dir que la cua de la distribució de Yule-Simon compleix en realitat la llei de Zipf, i ${\displaystyle f(k;\rho )}$ es pot utilitzar com a model, per exemple, de la freqüència relativa de la k-èsima paraula més freqüent en un text llarg, que segons la llei de Zipf és inversament proporcional a una (generalment petita) potència de k.

La distribució de Yule-Simon va sorgir originalment com la distribució limitant d'un procés estocàstic particular, estudiat per Yule com a model per a la distribució dels tàxons biològics i els subtàxons.^[3] Simon va nomenar aquest procés el "procés de Yule", però avui és més conegut com un procés de vinculació preferencial. El procés de vinculació preferencial és un procés urna en el que s'afegeixen les boles a un nombre creixent d'urnes, cada bola que s'assigna a una urna amb probabilitat lineal al nombre de l'urna que ja en conté.

La distribució també apareix com una distribució composta, en la que el paràmetre d'una distribució geomètrica es tracta com una funció de la variable aleatòria que té una distribució exponencial. Específicament, se suposa que W segueix una distribució exponencial amb l'escala 1/ρ o ratio ρ:

${\displaystyle W\sim \operatorname {Exponential} (\rho )}$,

amb funció densitat

${\displaystyle h(w;\rho )=\rho \exp(-\rho w)}$..

Llavors una variable K que segueixi la distribució de Yule-Simon té la següent distribució geomètrica condicional en W:

${\displaystyle K\sim \operatorname {Geometric} (\exp(-W))\,.}$

La fdp de una distribució geomètrica és:

${\displaystyle g(k;p)=p(1-p)^{k-1}}$

per a ${\displaystyle k\in \{1,2,\dotsc \}}$. La funció densitat de probabilitat és la següent distribució composta exponencial-geomètrica:

${\displaystyle f(k;\rho )=\int _{0}^{\infty }g(k;\exp(-w))h(w;\rho )\,dw}$.

amb la següent relació de recurrència:

${\displaystyle \left\{{\begin{array}{l}kP(k)=(\alpha +k+1)P(k+1),\\[10pt]P(1)=\alpha B(\alpha +1,1)\end{array}}\right\}}$

La generalització dels dos paràmetres de la distribució de Yule porten a reemplaçar la funció beta per una funció beta incompleta. La funció densitat de probabilitat de la distribució de Yule-Simon generalitzada (ρ, α) es defineix com:

${\displaystyle f(k;\rho ,\alpha )={\frac {\rho }{1-\alpha ^{\rho }}}\;\mathrm {B} _{1-\alpha }(k,\rho +1)}$

amb 0 ⩽ α < 1. Per a α = 0 s'obté com un cas particular la distribució ordinària de Yule-Simon (ρ). L'ús de la funció beta incompleta té l'efecte d'introduir un límit exponencial de la cua superior.

• Colin Rose and Murray D. Smith, "Mathematical Statistics with Mathematica". New York: Springer, 2002, ISBN 0-387-95234-9