Projektion (Lineare Algebra)

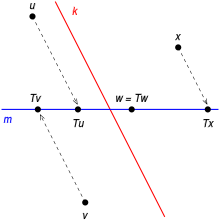
In der Mathematik ist eine Projektion oder ein Projektor eine spezielle lineare Abbildung (Endomorphismus) über einem Vektorraum ${\displaystyle V}$, die alle Vektoren in ihrem Bild (ein Unterraum von ${\displaystyle V}$) unverändert lässt.

Bei geeigneter Wahl einer Basis von ${\displaystyle V}$ setzt die Projektion einige Komponenten eines Vektors auf null und behält die übrigen bei. Damit ist auch anschaulich die Bezeichnung Projektion gerechtfertigt, wie etwa bei der Abbildung eines Hauses in einem zweidimensionalen Grundriss.

Sei ${\displaystyle V}$ ein Vektorraum. Ein Vektorraum-Endomorphismus ${\displaystyle P\colon V\to V}$ heißt Projektion, falls er idempotent ist, also wenn ${\displaystyle P\circ P=P}$ gilt.

Eine Projektion kann nur die Zahlen 0 und 1 als Eigenwert haben. Die Eigenräume sind

• ${\displaystyle \ker P}$ (Kern von ${\displaystyle P}$) zum Eigenwert 0 und
• ${\displaystyle \operatorname {im} P}$ (Bild von ${\displaystyle P}$) zum Eigenwert 1.

Der gesamte Raum ist die direkte Summe dieser beiden Untervektorräume:

${\displaystyle V=\ker P\oplus \operatorname {im} P}$

Die Abbildung ${\displaystyle P}$ ist anschaulich gesprochen eine Parallelprojektion auf ${\displaystyle \operatorname {im} P}$ entlang ${\displaystyle \ker P}$.

Ist ${\displaystyle P}$ eine Projektion, so ist auch ${\displaystyle \operatorname {id} -P}$ eine Projektion, und es gilt:

${\displaystyle \ker P=\operatorname {im} (\operatorname {id} -P)}$

${\displaystyle \operatorname {im} P=\ker(\operatorname {id} -P)}$

Ist ${\displaystyle V}$ ein Vektorraum und ${\displaystyle U}$ ein Unterraum, so gibt es im Allgemeinen viele Projektionen auf ${\displaystyle U}$, d. h. Projektionen, deren Bild ${\displaystyle U}$ ist. Ist ${\displaystyle P}$ eine Projektion mit Bild ${\displaystyle U}$, so ist ${\displaystyle \ker P}$ ein Komplement zu ${\displaystyle U}$ in ${\displaystyle V}$.

Ist umgekehrt ${\displaystyle W}$ ein Komplement von ${\displaystyle U}$ in ${\displaystyle V}$, also ${\displaystyle V=U\oplus W}$, so lässt sich jedes ${\displaystyle v\in V}$ als Summe ${\displaystyle v=u+w}$ mit eindeutig bestimmten ${\displaystyle u\in U}$ und ${\displaystyle w\in W}$ darstellen. Der Endomorphismus von ${\displaystyle V}$, der jedem ${\displaystyle v}$ das zugehörige ${\displaystyle u}$ zuordnet, ist eine Projektion mit Bild ${\displaystyle U}$ und Kern ${\displaystyle W}$. Projektionen und Zerlegungen in komplementäre Unterräume entsprechen einander also.

Ist ${\displaystyle V}$ ein endlichdimensionaler reeller oder komplexer Vektorraum mit einem Skalarprodukt, so gibt es zu jedem Untervektorraum ${\displaystyle U}$ die Projektion entlang des orthogonalen Komplements von ${\displaystyle U}$, die „Orthogonalprojektion auf ${\displaystyle U}$“ genannt wird. Sie ist die eindeutig bestimmte lineare Abbildung ${\displaystyle P\colon V\to V}$ mit der Eigenschaft, dass für alle ${\displaystyle v\in V}$

• ${\displaystyle P(v)\in U}$ und
• ${\displaystyle v-P(v)\perp U}$

gilt.

Ist ${\displaystyle V}$ ein unendlichdimensionaler Hilbertraum, so gilt diese Aussage mit dem Projektionssatz entsprechend auch für abgeschlossene Untervektorräume ${\displaystyle U}$. In diesem Fall kann ${\displaystyle P}$ stetig gewählt werden.

Als einfache Beispiele lassen sich für jeden Vektorraum ${\displaystyle V}$ die Identität ${\displaystyle Id:v\mapsto v}$ und die Abbildung ${\displaystyle N\colon v\mapsto 0}$ für ${\displaystyle v\in V}$ als triviale Projektionen angeben (die sich durch die Einheits- bzw. Nullmatrix darstellen lassen).

Es sei ${\displaystyle P}$ die Abbildung der Ebene ${\displaystyle \mathbb {R} ^{2}}$ in sich, die durch die Matrix

${\displaystyle P={\begin{pmatrix}1&0\\0&0\end{pmatrix}}}$

beschrieben ist. Sie projiziert einen Vektor ${\displaystyle {\tbinom {x}{y}}}$ auf ${\displaystyle {\tbinom {x}{0}}}$, also orthogonal auf die x-Achse. Der Eigenraum zum Eigenwert ${\displaystyle 0}$, also der Kern, wird von ${\displaystyle {\tbinom {0}{1}}}$, der Eigenraum zum Eigenwert ${\displaystyle 1}$, also das Bild, wird von ${\displaystyle {\tbinom {1}{0}}}$ aufgespannt. Der Projektor ${\displaystyle \operatorname {id} -P}$ ist die orthogonale Projektion auf die y-Achse.

Dagegen ist beispielsweise die durch die Matrix

${\displaystyle P={\begin{pmatrix}1&-1\\0&0\end{pmatrix}}}$

beschriebene Abbildung der Ebene zwar wegen ${\displaystyle P^{2}=P}$ ebenfalls eine Projektion, allerdings keine orthogonale Projektion. Ihr Bild ist wiederum die x-Achse, ihr Kern ist jedoch die Gerade mit der Gleichung ${\displaystyle y=x}$.

In der Quantenmechanik spricht man im Zusammenhang mit dem Messprozess von einer Projektion des Zustandsvektors ψ, wobei die präzise Interpretation im Folgenden beschrieben wird:

• Als Messergebnis kommt nur einer der i. A. unendlich vielen sog. Eigenwerte der betrachteten Observablen infrage (d. h. des zugeordneten selbstadjungierten Operators im Zustandsraum des Systems, dem sog. Hilbertraum). Die Auswahl erfolgt zufällig (Kopenhagener Interpretation) mit einer gewissen Wahrscheinlichkeit, die hier nicht benötigt wird.
• Die Berechnung der Wahrscheinlichkeit für einen Eigenwert (Messergebnis) erfolgt u. a. mithilfe der Projektion auf dessen Eigenraum.

Die Gesamtheit der so erhaltenen Projektionsoperatoren ist, bei gegebener Messgröße, „vollständig“ und ergibt die sog. Spektraldarstellung der Observablen.

• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
• Dirk Werner: Funktionalanalysis. 6., korrigierte Auflage, Springer-Verlag, Berlin 2007, ISBN 978-3-540-72533-6, Seite 161.