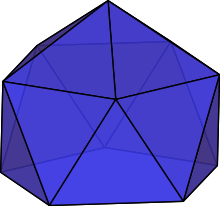
Gyroelongated pentagonal pyramid

11th Johnson solid (16 faces)

Gyroelongated pentagonal pyramid

Type	Johnson J₁₀ – J₁₁ – J₁₂
Faces	15 triangles 1 pentagon
Edges	25
Vertices	11
Vertex configuration	5(3³.5) 1+5(3⁵)
Symmetry group	$C_{5\mathrm {v} }$
Properties	convex
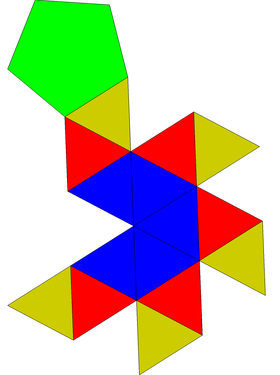
Net

In geometry, the gyroelongated pentagonal pyramid is a polyhedron constructed by attaching a pentagonal antiprism to the base of a pentagonal pyramid. An alternative name is diminished icosahedron because it can be constructed by removing a pentagonal pyramid from a regular icosahedron.

Construction

The gyroelongated pentagonal pyramid can be constructed from a pentagonal antiprism by attaching a pentagonal pyramid onto its pentagonal face.^[1] This pyramid covers the pentagonal faces, so the resulting polyhedron has 15 equilateral triangles and 1 regular pentagon as its faces.^[2] Another way to construct it is started from the regular icosahedron by cutting off one of two pentagonal pyramids, a process known as diminishment; for this reason, it is also called the diminished icosahedron.^[3] Because the resulting polyhedron has the property of convexity and its faces are regular polygons, the gyroelongated pentagonal pyramid is a Johnson solid, enumerated as the 11th Johnson solid $J_{11}$ .^[4]

Properties

The surface area of a gyroelongated pentagonal pyramid $A$ can be obtained by summing the area of 15 equilateral triangles and 1 regular pentagon. Its volume $V$ can be ascertained either by slicing it off into both a pentagonal antiprism and a pentagonal pyramid, after which adding them up; or by subtracting the volume of a regular icosahedron to a pentagonal pyramid. With edge length $a$ , they are:^[2] ${\begin{aligned}A&={\frac {15{\sqrt {3}}+{\sqrt {5(5+2{\sqrt {5}})}}}{4}}a^{2}\approx 8.215a^{2},\\V&={\frac {25+9{\sqrt {5}}}{24}}a^{3}\approx 1.880a^{3}.\end{aligned}}$

It has the same three-dimensional symmetry group as the pentagonal pyramid: the cyclic group $C_{5\mathrm {v} }$ of order 10. Its dihedral angle can be obtained by involving the angle of a pentagonal antiprism and pentagonal pyramid: its dihedral angle between triangle-to-pentagon is the pentagonal antiprism's angle between that 100.8°, and its dihedral angle between triangle-to-triangle is the pentagonal pyramid's angle 138.2°.^[5]

References

^ Rajwade, A. R. (2001), Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem, Texts and Readings in Mathematics, Hindustan Book Agency, pp. 84–89, doi:10.1007/978-93-86279-06-4, ISBN 978-93-86279-06-4.
^ ^a ^b Berman, Martin (1971), "Regular-faced convex polyhedra", Journal of the Franklin Institute, 291 (5): 329–352, doi:10.1016/0016-0032(71)90071-8, MR 0290245.
^ Hartshorne, Robin (2000), Geometry: Euclid and Beyond, Undergraduate Texts in Mathematics, Springer-Verlag, p. 457, ISBN 9780387986500.
^ Uehara, Ryuhei (2020), Introduction to Computational Origami: The World of New Computational Geometry, Springer, p. 62, doi:10.1007/978-981-15-4470-5, ISBN 978-981-15-4470-5, S2CID 220150682.
^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603; see table III, line 11.