Flujo elemental
Flujo elemental es una colección de flujos básicos a partir de los cuales es posible construir flujos más complejos por superposición. Algunos de los flujos reflejan casos específicos y restricciones como incompresible o irrotacional, o ambos, como en el caso del flujo potencial.[1]
Flujo uniforme bidimensional
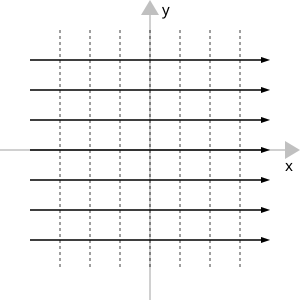
Dada una velocidad uniforme de un fluido en cualquier posición del espacio:
Este flujo es incompresible porque la velocidad es constante, las primeras derivadas de las componentes de la velocidad son cero y la divergencia total es cero:
Dado que la circulación es siempre cero el flujo es también irrotacional, podemos deducirlo del teorema de la circulación de Kelvin y del cálculo explícito de la vorticidad:
Al ser incompresible y bidimensional, este flujo se construye a partir de una función de flujo:
de donde
y en coordenadas cilíndricas
de donde
Como es habitual la función de flujo está definida hasta un valor constante que aquí tomamos como cero. También podemos confirmar que el flujo es irrotacional a partir de:
Siendo irrotacional, la función potencial es en cambio:
y por lo tanto
Fuente bidimensional de líneas de flujo

El caso de una línea vertical que emite a velocidad fija una cantidad constante de fluido Q por unidad de longitud es una fuente lineal. El problema tiene una simetría cilíndrica y puede tratarse en dos dimensiones en el plano ortogonal.
Las fuentes lineales y los sumideros lineales (abajo) son flujos elementales importantes porque desempeñan el papel de monopolo(s) para fluidos incompresibles (que también pueden considerarse ejemplos de campos solenoidales es decir, campos libres de divergencia). Los patrones de flujo genéricos también pueden descomponerse en términos de expansión multipolar, del mismo modo que para los campos eléctrico y magnético, donde el monopolo es esencialmente el primer término no trivial (por ejemplo, constante) de la expansión.
Este patrón de flujo también es irrotacional e incompresible.
Se caracteriza por una simetría cilíndrica:|
Donde el flujo total saliente es constante
Por lo tanto,
Se deriva de una función de flujoion
o de una función potencial
Sumidero de línea bidimensional
El caso de una línea vertical que absorbe a un ritmo fijo una cantidad constante de fluido Q por unidad de longitud es un sumidero lineal. Todo es igual al caso de una línea fuente a parte del signo negativo. Esto se deriva de una función de flujo
o a partir de una función potencial
Dado que los dos resultados son iguales a una parte de un signo menos, podemos tratar de forma transparente tanto las fuentes como los sumideros lineales con la misma corriente y funciones potenciales permitiendo que Q asuma tanto valores positivos como negativos y quitando el signo menos en la definición de Q.
Doblete bidimensional o fuente de línea dipolar

Si consideramos una línea fuente y una línea sumidero a una distancia d podemos reutilizar los resultados anteriores y la función de flujo será
La última aproximación es de primer orden en d.
Dado
Queda
La velocidad es entonces
Y el potencial en cambio
Línea de vórtice bidimensional

Este es el caso de un filamento de vórtice que gira a velocidad constante, existe una simetría cilíndrica y el problema puede resolverse en el plano ortogonal.
Al igual que en el caso anterior de las fuentes lineales, las líneas de vórtice desempeñan el papel de monopolos para flujo irrotacional.
También en este caso el flujo es a la vez irrotacional e incompresible y por lo tanto un caso de flujo potencial.
Se caracteriza por una simetría cilíndrica:
Donde la circulación total es constante para cada línea cerrada alrededor del vórtice central
y es cero para cualquier línea que no incluya el vórtice.
Por lo tanto,
Esto se deriva de una función de corriente
o de una función potencial
Que es dual al caso anterior de una fuente lineal
Flujo potencial bidimensional genérico
Dado un flujo bidimensional incompresible que además es irrotacional tenemos:
Que es en coordenadas cilíndricas[2]
Buscamos una solución con variables separadas:
lo que da
Dado que la parte izquierda sólo depende de r y la parte derecha sólo depende de , las dos partes deben ser iguales a una constante independiente de r y . La constante será positiva. Por tanto,
La solución de la segunda ecuación es una combinación lineal de y . Para tener una velocidad de un solo valor (y también una función de corriente de un solo valor) m debe ser un número entero positivo.
Por lo tanto la solución más genérica viene dada por
En cambio, el potencial viene dado por
Referencias
Bibliografía
- Fitzpatrick, Richard (2017), Theoretical fluid dynamics, IOP science, ISBN 978-0-7503-1554-8 .
- Faber, T.E. (1995), Fluid Dynamics for Physicists, Cambridge university press, ISBN 9780511806735 .
Bibliografía adicional
- Batchelor, G.K. (1973), An introduction to fluid dynamics, Cambridge University Press, ISBN 978-0-521-09817-5 .
- Chanson, H. (2009), Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows, CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages, ISBN 978-0-415-49271-3 .
- Lamb, H. (1994) [1932], Hydrodynamics (6th edición), Cambridge University Press, ISBN 978-0-521-45868-9 .
- Milne-Thomson, L.M. (1996) [1968], Theoretical hydrodynamics (5th edición), Dover, ISBN 978-0-486-68970-8 .
Enlaces externos
- Richard Fitzpatrick University of Texas, Austin (2017). «Fluid Mechanics». University of Texas, Austin. Consultado el 7 de febrero de 2018.
- (c) Aerospace, Mechanical & Mechatronic Engg. 2005 University of Sydney (2005). «Elements of Potential Flow». University of Sydney. Consultado el 19 de abril de 2019.
 Datos: Q48817327
Datos: Q48817327





















![{\displaystyle \mathbf {d} =d[\cos(\theta _{0})\mathbf {e} _{x}+\sin(\theta _{0})\mathbf {e} _{y}]=d[\cos(\theta -\theta _{0})\mathbf {e} _{r}+\sin(\theta -\theta _{0})\mathbf {e} _{\theta }].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/507b9af4a87a5fa25472bca530792342321e6d78)

















![{\displaystyle \psi =\alpha _{0}+\beta _{0}\ln r+\sum _{m>0}{\left(\alpha _{m}r^{m}+\beta _{m}r^{-m}\right)\sin {[m(\theta -\theta _{m})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91e2e00a53ef74b71c0c182739700e67630247bd)
![{\displaystyle \phi =\alpha _{0}-\beta _{0}\theta +\sum _{m\mathop {>} 0}{(\alpha _{m}r^{m}-\beta _{m}r^{-m})\cos {[m(\theta -\theta _{m})]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ae11d9c0fa83d2856902127f9cd620c057980ee)









