Loi du χ

Loi du ${\displaystyle \chi }$
Densité de probabilité
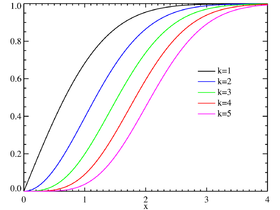
Fonction de répartition
Paramètres	${\displaystyle k\in \{1,2,\dots \}\,}$ (degrés de liberté)
Support	${\displaystyle x\in [0;\infty [}$
Densité de probabilité	${\displaystyle {\frac {2^{1-k/2}x^{k-1}e^{-x^{2}/2}}{\Gamma (k/2)}}}$
Fonction de répartition	${\displaystyle P(k/2,x^{2}/2)\,}$
Espérance	${\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ((k+1)/2)}{\Gamma (k/2)}}}$
Mode	${\displaystyle {\sqrt {k-1}}\,}$ pour ${\displaystyle k\geq 1}$
Variance	${\displaystyle \sigma ^{2}=k-\mu ^{2}\,}$
Asymétrie	${\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}$
Kurtosis normalisé	${\displaystyle {\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}$
Entropie	${\displaystyle \ln(\Gamma (k/2))+\,}$ ${\displaystyle \,{\frac {1}{2}}(k\!-\!\ln(2)\!-\!(k\!-\!1)\psi _{0}(k/2))}$
Fonction génératrice des moments	(voir détails dans l'article)
Fonction caractéristique	(voir détails dans l'article)
modifier

En théorie des probabilités et en statistique, la loi du ${\displaystyle \chi }$ (prononcer « khi ») est une loi de probabilité continue. C'est la loi de la moyenne quadratique de k variables aléatoires indépendantes de loi normale centrée réduite, le paramètre k est le nombre de degrés de liberté. L'exemple le plus courant est la loi de Maxwell, pour k=3 degrés de liberté d'une loi du ${\displaystyle \chi }$ ; elle modélise la vitesse moléculaire (normalisée).

Si ${\displaystyle X_{i}}$ sont k variables aléatoires indépendantes de loi normale avec pour moyenne ${\displaystyle \mu _{i}}$ et écart-type ${\displaystyle \sigma _{i}}$, alors la variable

${\displaystyle Y={\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}$

est de loi du ${\displaystyle \chi }$.

La densité de probabilité de la loi du ${\displaystyle \chi }$ est :

${\displaystyle f(x;k)={\begin{cases}\displaystyle {\frac {2^{1-{\frac {k}{2}}}x^{k-1}e^{-{\frac {x^{2}}{2}}}}{\Gamma ({\frac {k}{2}})}}&{\text{ pour }}x>0\\0&{\text{ sinon}}\end{cases}}}$

où ${\displaystyle \Gamma (z)}$ est la fonction gamma.

La fonction de répartition de la loi du ${\displaystyle \chi }$ est :

${\displaystyle F(x;k)={\begin{cases}\displaystyle P\left({\frac {k}{2}},{\frac {x^{2}}{2}}\right)&{\text{ pour }}x>0\\0&{\text{ sinon}}\end{cases}}}$

où ${\displaystyle P(k,x)}$ est la fonction gamma incomplète (régularisée).

La fonction génératrice des moments est donnée par :

${\displaystyle M(t)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {t^{2}}{2}}\right)+t{\sqrt {2}}\,{\frac {\Gamma ({\tfrac {k+1}{2}})}{\Gamma ({\tfrac {k}{2}})}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {t^{2}}{2}}\right).}$

où M est la fonction hypergéométrique confluente de Kummer.

La fonction caractéristique est donnée par :

${\displaystyle \varphi (t;k)=M\left({\frac {k}{2}},{\frac {1}{2}},{\frac {-t^{2}}{2}}\right)+it{\sqrt {2}}\,{\frac {\Gamma ({\tfrac {k+1}{2}})}{\Gamma ({\tfrac {k}{2}})}}M\left({\frac {k+1}{2}},{\frac {3}{2}},{\frac {-t^{2}}{2}}\right).}$

où M est encore la fonction hypergéométrique confluente de Kummer.

Les moments de la loi du ${\displaystyle \chi }$ sont donnés par :

${\displaystyle \mu _{j}=2^{j/2}{\frac {\Gamma ({\tfrac {k+j}{2}})}{\Gamma ({\tfrac {k}{2}})}}}$

où ${\displaystyle \Gamma (z)}$ est la fonction gamma. Les premiers moments sont :

${\displaystyle \mu _{1}={\sqrt {2}}\,\,{\frac {\Gamma ({\tfrac {k+1}{2}})}{\Gamma ({\tfrac {k}{2}})}}}$

${\displaystyle \mu _{2}=k\,}$

${\displaystyle \mu _{3}=2{\sqrt {2}}\,\,{\frac {\Gamma ({\tfrac {k+3}{2}})}{\Gamma ({\tfrac {k}{2}})}}=(k+1)\mu _{1}}$

${\displaystyle \mu _{4}=k(k+2)\,}$

${\displaystyle \mu _{5}=4{\sqrt {2}}\,\,{\frac {\Gamma ({\tfrac {k+5}{2}})}{\Gamma ({\tfrac {k}{2}})}}=(k+1)(k+3)\mu _{1}}$

${\displaystyle \mu _{6}=k(k+2)(k+4)\,}$

où les expressions sont issues de la relation de récurrence de la fonction gamma :

${\displaystyle \Gamma (x+1)=x\Gamma (x)\,}$

à partir de ces expressions, on peut établir les relations suivantes pour l'espérance, la variance, l'asymétrie et enfin le kurtosis :

${\displaystyle \mu ={\sqrt {2}}\,{\frac {\Gamma ({\tfrac {k+1}{2}})}{\Gamma ({\tfrac {k}{2}})}}}$

${\displaystyle \sigma ^{2}=k-\mu ^{2}\,}$

${\displaystyle \gamma _{1}={\frac {\mu }{\sigma ^{3}}}\,(1-2\sigma ^{2})}$

${\displaystyle \gamma _{2}={\frac {2}{\sigma ^{2}}}(1-\mu \sigma \gamma _{1}-\sigma ^{2})}$

L'entropie est donnée par :

${\displaystyle S=\ln \left(\Gamma \left({\frac {k}{2}}\right)\right)+{\frac {1}{2}}\left(k-\ln(2)-(k-1)\psi _{0}\left({\frac {k}{2}}\right)\right)}$

où ${\displaystyle \psi _{0}(z)}$ est la fonction polygamma.

• Si ${\displaystyle X\sim \chi _{k}(x)}$ alors ${\displaystyle X^{2}\sim \chi _{k}^{2}}$, (loi du χ²)
• ${\displaystyle \lim _{k\to \infty }{\tfrac {\chi _{k}(x)-\mu _{k}}{\sigma _{k}}}{\xrightarrow {d}}\ N(0,1)\,}$, (loi normale)
• Si ${\displaystyle X\sim \chi _{1}(x)\,}$ alors ${\displaystyle \sigma X\sim HN(\sigma )\,}$, (loi demi-normale) pour tout ${\displaystyle \sigma >0\,}$
• ${\displaystyle \chi _{2}(x)\sim \mathrm {Rayleigh} (1)\,}$, (loi de Rayleigh)
• ${\displaystyle \chi _{3}(x)\sim \mathrm {Maxwell} (1)\,}$, (loi de Maxwell)
• ${\displaystyle \|{\boldsymbol {N}}_{i=1,\ldots ,k}{(0,1)}\|\sim \chi _{k}(x)}$, (la norme de n variables de loi normale est de loi du ${\displaystyle \chi }$à k degrés de liberté.)
• la loi du ${\displaystyle \chi }$ est un cas particulier de la loi Gamma généralisée.

Différentes lois du ${\displaystyle \chi }$ et ${\displaystyle \chi ^{2}}$

Lois	en fonction de variables de loi normale
loi du χ²	${\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}$
loi du χ² non centrée	${\displaystyle \sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}$
loi du χ	${\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}-\mu _{i}}{\sigma _{i}}}\right)^{2}}}}$
loi du χ non centrée	${\displaystyle {\sqrt {\sum _{i=1}^{k}\left({\frac {X_{i}}{\sigma _{i}}}\right)^{2}}}}$

• (en) Eric W. Weisstein, « Chi Distribution », sur MathWorld

• Portail des probabilités et de la statistique